Equiv: Bioequivalence in a Cross-Over Trial¶

An example from OpenBUGS [44] and Gelfand et al. [29] concerning a two-treatment, cross-over trial with 10 subjects.

Model¶

Treatment responses are modelled as

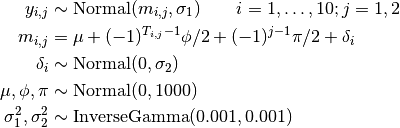
$y_{i,j} &\sim \text{Normal}(m_{i,j}, \sigma_1) \quad\quad i=1,\ldots,10; j=1,2 \\ m_{i,j} &= \mu + (-1)^{T_{i,j} - 1} \phi / 2 + (-1)^{j-1} \pi / 2 + \delta_i \\ \delta_i &\sim \text{Normal}(0, \sigma_2) \\ \mu, \phi, \pi &\sim \text{Normal}(0, 1000) \\ \sigma_1^2, \sigma_2^2 &\sim \text{InverseGamma}(0.001, 0.001) \\$

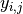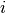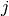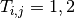where $y_{i,j}$ is the response for patient $i$ in period $j$ ; and $T_{i,j} = 1,2$ is the treatment received.

Analysis Program¶

using Mamba

## Data
equiv = Dict{Symbol, Any}(
  :group => [1, 1, 2, 2, 2, 1, 1, 1, 2, 2],
  :y =>
    [1.40 1.65
     1.64 1.57
     1.44 1.58
     1.36 1.68
     1.65 1.69
     1.08 1.31
     1.09 1.43
     1.25 1.44
     1.25 1.39
     1.30 1.52]
)
equiv[:N] = size(equiv[:y], 1)
equiv[:P] = size(equiv[:y], 2)

equiv[:T] = [equiv[:group] 3 - equiv[:group]]


## Model Specification
model = Model(

  y = Stochastic(2,
    (delta, mu, phi, pi, s2_1, T) ->
      begin
        sigma = sqrt(s2_1)
        UnivariateDistribution[
          begin
            m = mu + (-1)^(T[i, j] - 1) * phi / 2 + (-1)^(j - 1) * pi / 2 +
                delta[i, j]
            Normal(m, sigma)
          end
          for i in 1:10, j in 1:2
        ]
      end,
    false
  ),

  delta = Stochastic(2,
    s2_2 -> Normal(0, sqrt(s2_2)),
    false
  ),

  mu = Stochastic(
    () -> Normal(0, 1000)
  ),

  phi = Stochastic(
    () -> Normal(0, 1000)
  ),

  theta = Logical(
    phi -> exp(phi)
  ),

  pi = Stochastic(
    () -> Normal(0, 1000)
  ),

  s2_1 = Stochastic(
    () -> InverseGamma(0.001, 0.001)
  ),

  s2_2 = Stochastic(
    () -> InverseGamma(0.001, 0.001)
  ),

  equiv = Logical(
    theta -> Int(0.8 < theta < 1.2)
  )

)


## Initial Values
inits = [
  Dict(:y => equiv[:y], :delta => zeros(10, 2), :mu => 0, :phi => 0,
       :pi => 0, :s2_1 => 1, :s2_2 => 1),
  Dict(:y => equiv[:y], :delta => zeros(10, 2), :mu => 10, :phi => 10,
       :pi => 10, :s2_1 => 10, :s2_2 => 10)
]


## Sampling Scheme
scheme = [NUTS(:delta),
          Slice([:mu, :phi, :pi], 1.0),
          Slice([:s2_1, :s2_2], 1.0, Univariate)]
setsamplers!(model, scheme)


## MCMC Simulations
sim = mcmc(model, equiv, inits, 12500, burnin=2500, thin=2, chains=2)
describe(sim)

Results¶

Iterations = 2502:12500
Thinning interval = 2
Chains = 1,2
Samples per chain = 5000

Empirical Posterior Estimates:
           Mean          SD        Naive SE       MCSE         ESS
 s2_2  0.0173121833 0.014549568 0.00014549568 0.0007329722  394.02626
 s2_1  0.0184397014 0.013837972 0.00013837972 0.0005689492  591.55873
   pi -0.1874240524 0.086420302 0.00086420302 0.0032257037  717.76558
  phi -0.0035569545 0.087590520 0.00087590520 0.0035141650  621.25503
theta  1.0002921934 0.088250458 0.00088250458 0.0036227671  593.40761
equiv  0.9751000000 0.155828169 0.00155828169 0.0036666529 1806.14385
   mu  1.4387396416 0.042269208 0.00042269208 0.0013735876  946.96847

Quantiles:
           2.5%         25.0%         50.0%        75.0%        97.5%
 s2_2  0.0016375061  0.0056159514  0.013968228  0.024613730  0.053154674
 s2_1  0.0017289114  0.0074958338  0.015849718  0.025963832  0.051967161
   pi -0.3579631753 -0.2432161807 -0.187946319 -0.130454165 -0.014910965
  phi -0.1723722017 -0.0623573600 -0.005681830  0.053144647  0.172913654
theta  0.8416658455  0.9395470702  0.994334281  1.054582177  1.188763456
equiv  1.0000000000  1.0000000000  1.000000000  1.000000000  1.000000000
   mu  1.3552569594  1.4110400018  1.438593809  1.466525521  1.519643109