Salm: Extra-Poisson Variation in a Dose-Response Study¶
An example from OpenBUGS [44] and Breslow [9] concerning mutagenicity assay data on salmonella in three plates exposed to six doses of quinoline.
Model¶
Number of revertant colonies of salmonella are modelled as
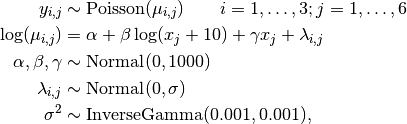
where 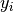 is the number of colonies in plate
is the number of colonies in plate 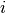 and dose
and dose 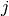 .
.
Analysis Program¶
using Mamba
## Data
salm = Dict{Symbol, Any}(
:y => reshape(
[15, 21, 29, 16, 18, 21, 16, 26, 33, 27, 41, 60, 33, 38, 41, 20, 27, 42],
3, 6),
:x => [0, 10, 33, 100, 333, 1000],
:plate => 3,
:dose => 6
)
## Model Specification
model = Model(
y = Stochastic(2,
(alpha, beta, gamma, x, lambda) ->
UnivariateDistribution[
begin
mu = exp(alpha + beta * log(x[j] + 10) + gamma * x[j] + lambda[i, j])
Poisson(mu)
end
for i in 1:3, j in 1:6
],
false
),
alpha = Stochastic(
() -> Normal(0, 1000)
),
beta = Stochastic(
() -> Normal(0, 1000)
),
gamma = Stochastic(
() -> Normal(0, 1000)
),
lambda = Stochastic(2,
s2 -> Normal(0, sqrt(s2)),
false
),
s2 = Stochastic(
() -> InverseGamma(0.001, 0.001)
)
)
## Initial Values
inits = [
Dict(:y => salm[:y], :alpha => 0, :beta => 0, :gamma => 0, :s2 => 10,
:lambda => zeros(3, 6)),
Dict(:y => salm[:y], :alpha => 1, :beta => 1, :gamma => 0.01, :s2 => 1,
:lambda => zeros(3, 6))
]
## Sampling Scheme
scheme = [Slice([:alpha, :beta, :gamma], [1.0, 1.0, 0.1]),
AMWG([:lambda, :s2], 0.1)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, salm, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
s2 0.0690769709 0.04304237136 0.000497010494 0.001985478741 469.961085
gamma -0.0011250515 0.00034536546 0.000003987937 0.000025419899 184.590851
beta 0.3543443166 0.07160779229 0.000826855563 0.007122805926 101.069088
alpha 2.0100584321 0.26156942610 0.003020343571 0.027100522461 93.157673
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
s2 0.0135820292 0.039788136 0.0598307554 0.08740879470 0.17747300708
gamma -0.0017930379 -0.001347435 -0.0011325733 -0.00090960998 -0.00039271486
beta 0.2073237562 0.312747679 0.3582979574 0.40006921583 0.48789037325
alpha 1.5060295212 1.847111545 2.0062727893 2.16556036713 2.50547846044