Birats: A Bivariate Normal Hierarchical Model¶
An example from OpenBUGS [44] and section 6 of Gelfand et al. [29] concerning 30 rats whose weights were measured at each of five consecutive weeks.
Model¶
Weights are modeled as
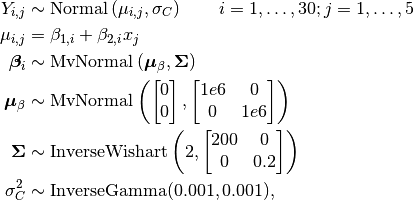
where 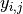 is repeated weight measurement
is repeated weight measurement 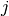 on rat
on rat 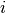 , and
, and 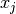 is the day on which the measurement was taken.
is the day on which the measurement was taken.
Analysis Program¶
using Mamba
## Data
birats = Dict{Symbol, Any}(
:N => 30, :T => 5,
:x => [8.0, 15.0, 22.0, 29.0, 36.0],
:Y => [151 199 246 283 320
145 199 249 293 354
147 214 263 312 328
155 200 237 272 297
135 188 230 280 323
159 210 252 298 331
141 189 231 275 305
159 201 248 297 338
177 236 285 350 376
134 182 220 260 296
160 208 261 313 352
143 188 220 273 314
154 200 244 289 325
171 221 270 326 358
163 216 242 281 312
160 207 248 288 324
142 187 234 280 316
156 203 243 283 317
157 212 259 307 336
152 203 246 286 321
154 205 253 298 334
139 190 225 267 302
146 191 229 272 302
157 211 250 285 323
132 185 237 286 331
160 207 257 303 345
169 216 261 295 333
157 205 248 289 316
137 180 219 258 291
153 200 244 286 324],
:mean => [0.0, 0.0],
:var => [1.0e6 0.0
0.0 1.0e6],
:Omega => [200.0 0.0
0.0 0.2]
)
## Model Specification
model = Model(
Y = Stochastic(2,
(beta, x, sigmaC, N, T) ->
UnivariateDistribution[
Normal(beta[i, 1] + beta[i, 2] * x[j], sigmaC)
for i in 1:N, j in 1:T
],
false
),
beta = Stochastic(2,
(mu_beta, Sigma, N) ->
MultivariateDistribution[
MvNormal(mu_beta, Sigma)
for i in 1:N
],
false
),
mu_beta = Stochastic(1,
(mean, var) -> MvNormal(mean, var)
),
Sigma = Stochastic(2,
Omega -> InverseWishart(2, Omega),
false
),
sigma2C = Stochastic(
() -> InverseGamma(0.001, 0.001),
false
),
sigmaC = Logical(
sigma2C -> sqrt(sigma2C)
)
)
## Initial Values
inits = [
Dict(:Y => birats[:Y], :beta => repmat([100 6], birats[:N], 1),
:mu_beta => [0, 0], :Sigma => eye(2), :sigma2C => 1.0),
Dict(:Y => birats[:Y], :beta => repmat([50 3], birats[:N], 1),
:mu_beta => [10, 10], :Sigma => 0.3 * eye(2), :sigma2C => 10.0)
]
## Sampling Scheme
scheme = [AMWG([:beta, :mu_beta], repmat([10.0, 1.0], birats[:N] + 1)),
AMWG(:Sigma, 1.0),
Slice(:sigma2C, 10.0)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, birats, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
mu_beta[1] 106.7046188 2.258246468 0.0260759841 0.081338282 770.81949
mu_beta[2] 6.1804557 0.104047928 0.0012014420 0.004102793 643.14317
sigmaC 6.1431758 0.460583341 0.0053183583 0.021005830 480.76933
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
mu_beta[1] 102.3595659 105.2252185 106.6914834 108.164852 111.2001520
mu_beta[2] 5.9720904 6.1130035 6.1817455 6.248025 6.3848798
sigmaC 5.3167022 5.8123935 6.1206859 6.445419 7.0971249