Blocker: Random Effects Meta-Analysis of Clinical Trials¶
An example from OpenBUGS [44] and Carlin [15] concerning a meta-analysis of 22 clinical trials to prevent mortality after myocardial infarction.
Model¶
Events are modelled as

where 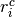 is the number of control group events, out of
is the number of control group events, out of 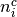 , in study
, in study 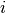 ; and
; and 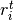 is the number of treatment group events.
is the number of treatment group events.
Analysis Program¶
using Mamba
## Data
blocker = Dict{Symbol, Any}(
:rt =>
[3, 7, 5, 102, 28, 4, 98, 60, 25, 138, 64, 45, 9, 57, 25, 33, 28, 8, 6, 32,
27, 22],
:nt =>
[38, 114, 69, 1533, 355, 59, 945, 632, 278, 1916, 873, 263, 291, 858, 154,
207, 251, 151, 174, 209, 391, 680],
:rc =>
[3, 14, 11, 127, 27, 6, 152, 48, 37, 188, 52, 47, 16, 45, 31, 38, 12, 6, 3,
40, 43, 39],
:nc =>
[39, 116, 93, 1520, 365, 52, 939, 471, 282, 1921, 583, 266, 293, 883, 147,
213, 122, 154, 134, 218, 364, 674]
)
blocker[:N] = length(blocker[:rt])
## Model Specification
model = Model(
rc = Stochastic(1,
(mu, nc, N) ->
begin
pc = invlogit.(mu)
UnivariateDistribution[Binomial(nc[i], pc[i]) for i in 1:N]
end,
false
),
rt = Stochastic(1,
(mu, delta, nt, N) ->
begin
pt = invlogit.(mu + delta)
UnivariateDistribution[Binomial(nt[i], pt[i]) for i in 1:N]
end,
false
),
mu = Stochastic(1,
() -> Normal(0, 1000),
false
),
delta = Stochastic(1,
(d, s2) -> Normal(d, sqrt(s2)),
false
),
delta_new = Stochastic(
(d, s2) -> Normal(d, sqrt(s2))
),
d = Stochastic(
() -> Normal(0, 1000)
),
s2 = Stochastic(
() -> InverseGamma(0.001, 0.001)
)
)
## Initial Values
inits = [
Dict(:rc => blocker[:rc], :rt => blocker[:rt], :d => 0, :delta_new => 0,
:s2 => 1, :mu => zeros(blocker[:N]), :delta => zeros(blocker[:N])),
Dict(:rc => blocker[:rc], :rt => blocker[:rt], :d => 2, :delta_new => 2,
:s2 => 10, :mu => fill(2, blocker[:N]), :delta => fill(2, blocker[:N]))
]
## Sampling Scheme
scheme = [AMWG(:mu, 0.1),
AMWG([:delta, :delta_new], 0.1),
Slice([:d, :s2], 1.0)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, blocker, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
s2 0.01822186 0.021121265 0.00024388736 0.0014150714 222.78358
d -0.25563567 0.061841945 0.00071408927 0.0040205781 236.58613
delta_new -0.25005767 0.150325282 0.00173580684 0.0050219145 896.03592
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
s2 0.0006855452 0.0041648765 0.0107615659 0.024442084 0.07735715
d -0.3734122953 -0.2959169814 -0.2581848849 -0.218341380 -0.12842580
delta_new -0.5385405488 -0.3279958446 -0.2557849252 -0.177588413 0.07986060