Magnesium: Meta-Analysis Prior Sensitivity¶
An example from OpenBUGS [44].
Model¶
Number of events reported for treatment and control subjects in 8 studies is modelled as
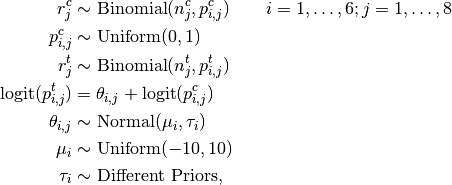
where 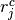 is the number of control group events, out of
is the number of control group events, out of 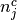 , in study
, in study 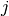 ;
; 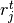 is the number of treatment group events; and
is the number of treatment group events; and 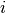 indexes differ prior specifications.
indexes differ prior specifications.
Analysis Program¶
using Mamba
## Data
magnesium = Dict{Symbol, Any}(
:rt => [1, 9, 2, 1, 10, 1, 1, 90],
:nt => [40, 135, 200, 48, 150, 59, 25, 1159],
:rc => [2, 23, 7, 1, 8, 9, 3, 118],
:nc => [36, 135, 200, 46, 148, 56, 23, 1157]
)
magnesium[:rtx] = hcat([magnesium[:rt] for i in 1:6]...)'
magnesium[:rcx] = hcat([magnesium[:rc] for i in 1:6]...)'
magnesium[:s2] = 1 ./ (magnesium[:rt] + 0.5) +
1 ./ (magnesium[:nt] - magnesium[:rt] + 0.5) +
1 ./ (magnesium[:rc] + 0.5) +
1 ./ (magnesium[:nc] - magnesium[:rc] + 0.5)
magnesium[:s2_0] = 1 / mean(1 ./ magnesium[:s2])
## Model Specification
model = Model(
rcx = Stochastic(2,
(nc, pc) ->
UnivariateDistribution[Binomial(nc[j], pc[i, j]) for i in 1:6, j in 1:8],
false
),
pc = Stochastic(2,
() -> Uniform(0, 1),
false
),
rtx = Stochastic(2,
(nt, pc, theta) ->
UnivariateDistribution[
begin
phi = logit(pc[i, j])
pt = invlogit(theta[i, j] + phi)
Binomial(nt[j], pt)
end
for i in 1:6, j in 1:8
],
false
),
theta = Stochastic(2,
(mu, tau) ->
UnivariateDistribution[Normal(mu[i], tau[i]) for i in 1:6, j in 1:8],
false
),
mu = Stochastic(1,
() -> Uniform(-10, 10),
false
),
OR = Logical(1,
mu -> exp.(mu)
),
tau = Logical(1,
(priors, s2_0) ->
Float64[
sqrt(priors[1]),
sqrt(priors[2]),
priors[3],
sqrt(s2_0 * (1 / priors[4] - 1)),
sqrt(s2_0) * (1 / priors[5] - 1),
sqrt(priors[6]) ]
),
priors = Stochastic(1,
s2_0 ->
UnivariateDistribution[
InverseGamma(0.001, 0.001),
Uniform(0, 50),
Uniform(0, 50),
Uniform(0, 1),
Uniform(0, 1),
Truncated(Normal(0, sqrt(s2_0 / erf(0.75))), 0, Inf)
],
false
)
)
## Initial Values
inits = [
Dict(:rcx => magnesium[:rcx], :rtx => magnesium[:rtx],
:theta => zeros(6, 8), :mu => fill(-0.5, 6),
:pc => fill(0.5, 6, 8), :priors => [1, 1, 1, 0.5, 0.5, 1]),
Dict(:rcx => magnesium[:rcx], :rtx => magnesium[:rtx],
:theta => zeros(6, 8), :mu => fill(0.5, 6),
:pc => fill(0.5, 6, 8), :priors => [1, 1, 1, 0.5, 0.5, 1])
]
## Sampling Scheme
scheme = [AMWG(:theta, 0.1),
AMWG(:mu, 0.1),
Slice(:pc, 0.25, Univariate),
Slice(:priors, [1.0, 5.0, 5.0, 0.25, 0.25, 5.0], Univariate)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, magnesium, inits, 12500, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:12500
Thinning interval = 2
Chains = 1,2
Samples per chain = 5000
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
tau[1] 0.55098858 0.35814901 0.0035814901 0.0221132365 262.31486
tau[2] 1.11557619 0.58886505 0.0058886505 0.0237788755 613.26606
tau[3] 0.83211110 0.49113676 0.0049113676 0.0222839957 485.75664
tau[4] 0.47864203 0.26258828 0.0026258828 0.0135868530 373.51920
tau[5] 0.48624861 0.35359386 0.0035359386 0.0215005369 270.46485
tau[6] 0.56841884 0.18877962 0.0018877962 0.0058505056 1041.17429
OR[1] 0.47784058 0.15389133 0.0015389133 0.0066922017 528.79852
OR[2] 0.42895913 0.32240192 0.0032240192 0.0081170895 1577.59150
OR[3] 0.43118350 0.18264467 0.0018264467 0.0064385836 804.69879
OR[4] 0.47587697 0.13947735 0.0013947735 0.0064893426 461.96170
OR[5] 0.48545299 0.14603013 0.0014603013 0.0083912319 302.85415
OR[6] 0.44554385 0.14121352 0.0014121352 0.0053818401 688.47941
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
tau[1] 0.050143630 0.28821905 0.49325476 0.73991793 1.42033542
tau[2] 0.326282292 0.70071249 0.98873505 1.39092470 2.65606546
tau[3] 0.136936046 0.49195419 0.74461372 1.06769203 2.03061696
tau[4] 0.091858771 0.28921566 0.44085251 0.61784984 1.10639558
tau[5] 0.028866916 0.23628679 0.42220429 0.65955432 1.37318750
tau[6] 0.214834142 0.43417486 0.56753402 0.70014948 0.94171060
OR[1] 0.206501871 0.37431326 0.47128600 0.57044051 0.80062151
OR[2] 0.107428346 0.27074745 0.38362516 0.52062237 0.99299623
OR[3] 0.145435475 0.30454141 0.41470065 0.53630024 0.83015778
OR[4] 0.231777387 0.38069803 0.47049713 0.56112444 0.76292805
OR[5] 0.207697044 0.38509504 0.48308284 0.59166588 0.75526778
OR[6] 0.208377218 0.34750042 0.43313882 0.52797553 0.76192141