Sampling Functions¶
Listed below are the sampling methods for which functions are provided to simulating draws from distributions that can be specified up to constants of proportionalities. Model-based Sampler constructors are available for use with the mcmc() engine as well as stand-alone functions that can be used independently.
- Approximate Bayesian Computation (ABC)
- Adaptive Mixture Metropolis (AMM)
- Adaptive Metropolis within Gibbs (AMWG)
- Binary Hamiltonian Monte Carlo (BHMC)
- Binary Individual Adaptation (BIA)
- Binary MCMC Model Composition (BMC3)
- Binary Metropolised Gibbs (BMG)
- Discrete Gibbs Sampler (DGS)
- Hamiltonian Monte Carlo (HMC)
- Metropolis-Adjusted Langevin Algorithm (MALA)
- Missing Values Sampler (MISS)
- No-U-Turn Sampler (NUTS)
- Random Walk Metropolis (RWM)
- Shrinkage Slice (Slice)
- Slice Simplex (SliceSimplex)
The following table summarizes the (d-dimensional) sample spaces over which each method simulates draws, whether draws are generated univariately or multivariately, and whether transformations are applied to map parameters to the sample spaces.
| Model-Based Constructors | Stand-Alone Functions | |||||
|---|---|---|---|---|---|---|
| Method | Sample Space | Univariate | Multivariate | Transformations | Univariate | Multivariate |
| ABC | 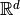 |
No | Yes | Yes | No | No |
| AMM | 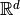 |
No | Yes | Yes | No | Yes |
| AMWG | 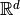 |
Yes | No | Yes | Yes | No |
| BHMC | 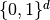 |
No | Yes | No | No | Yes |
| BIA | 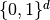 |
No | Yes | No | No | Yes |
| BMC3 | 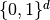 |
Yes | Yes | No | Yes | Yes |
| BMG | 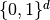 |
Yes | Yes | No | Yes | Yes |
| DGS | Finite 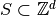 |
Yes | No | No | No | Yes |
| HMC | 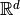 |
No | Yes | Yes | No | Yes |
| MALA | 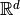 |
No | Yes | Yes | No | Yes |
| MISS | Parameter-defined | Yes | Yes | No | No | No |
| NUTS | 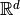 |
No | Yes | Yes | No | Yes |
| RWM | 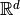 |
No | Yes | Yes | No | Yes |
| Slice | 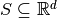 |
Yes | Yes | Optional | Yes | Yes |
| SliceSimplex | d-simplex | No | Yes | No | No | Yes |