Equiv: Bioequivalence in a Cross-Over Trial¶

An example from OpenBUGS [38] and Gelfand et al. [25] concerning a two-treatment, cross-over trial with 10 subjects.

Model¶

Treatment responses are modelled as

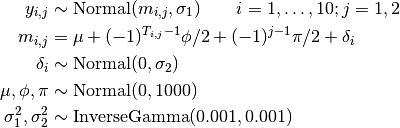
$y_{i,j} &\sim \text{Normal}(m_{i,j}, \sigma_1) \quad\quad i=1,\ldots,10; j=1,2 \\ m_{i,j} &= \mu + (-1)^{T_{i,j} - 1} \phi / 2 + (-1)^{j-1} \pi / 2 + \delta_i \\ \delta_i &\sim \text{Normal}(0, \sigma_2) \\ \mu, \phi, \pi &\sim \text{Normal}(0, 1000) \\ \sigma_1^2, \sigma_2^2 &\sim \text{InverseGamma}(0.001, 0.001) \\$

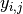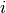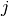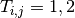where $y_{i,j}$ is the response for patient $i$ in period $j$ ; and $T_{i,j} = 1,2$ is the treatment received.

Analysis Program¶

using Mamba

## Data
equiv = (Symbol => Any)[
  :group => [1, 1, 2, 2, 2, 1, 1, 1, 2, 2],
  :y =>
    [1.40 1.65
     1.64 1.57
     1.44 1.58
     1.36 1.68
     1.65 1.69
     1.08 1.31
     1.09 1.43
     1.25 1.44
     1.25 1.39
     1.30 1.52]
]
equiv[:N] = size(equiv[:y], 1)
equiv[:P] = size(equiv[:y], 2)

equiv[:T] = [equiv[:group] 3 - equiv[:group]]


## Model Specification

model = Model(

  y = Stochastic(2,
    @modelexpr(delta, mu, phi, pi, s2_1, T,
      begin
        sigma = sqrt(s2_1)
        Distribution[
          begin
            m = mu + (-1)^(T[i,j]-1) * phi / 2 + (-1)^(j-1) * pi / 2 +
                delta[i,j]
            Normal(m, sigma)
          end
          for i in 1:10, j in 1:2
        ]
      end
    ),
    false
  ),

  delta = Stochastic(2,
    @modelexpr(s2_2,
      Normal(0, sqrt(s2_2))
    ),
    false
  ),

  mu = Stochastic(
    :(Normal(0, 1000))
  ),

  phi = Stochastic(
    :(Normal(0, 1000))
  ),

  theta = Logical(
    @modelexpr(phi,
      exp(phi)
    )
  ),

  pi = Stochastic(
    :(Normal(0, 1000))
  ),

  s2_1 = Stochastic(
    :(InverseGamma(0.001, 0.001))
  ),

  s2_2 = Stochastic(
    :(InverseGamma(0.001, 0.001))
  ),

  equiv = Logical(
    @modelexpr(theta,
      int(0.8 < theta < 1.2)
    )
  )

)


## Initial Values
inits = [
  [:y => equiv[:y], :delta => zeros(10, 2), :mu => 0, :phi => 0,
   :pi => 0, :s2_1 => 1, :s2_2 => 1],
  [:y => equiv[:y], :delta => zeros(10, 2), :mu => 10, :phi => 10,
   :pi => 10, :s2_1 => 10, :s2_2 => 10]
]


## Sampling Scheme
scheme = [NUTS([:delta]),
          Slice([:mu, :phi, :pi], fill(1.0, 3)),
          Slice([:s2_1, :s2_2], ones(2), :univar)]
setsamplers!(model, scheme)


## MCMC Simulations
sim = mcmc(model, equiv, inits, 12500, burnin=2500, thin=2, chains=2)
describe(sim)

Results¶

Iterations = 2502:12500
Thinning interval = 2
Chains = 1,2
Samples per chain = 5000

Empirical Posterior Estimates:
         Mean        SD       Naive SE       MCSE        ESS
   pi -0.1788624 0.07963600 0.0007963600 0.0022537740 1248.5276
   mu  1.4432301 0.04735444 0.0004735444 0.0020359933  540.9645
equiv  0.9835000 0.12739456 0.0012739456 0.0022978910 3073.5685
 s2_2  0.0187006 0.01466228 0.0001466228 0.0004799037  933.4580
 s2_1  0.0164033 0.01412396 0.0001412396 0.0005079176  773.2610
theta  0.9837569 0.07936595 0.0007936595 0.0025041274 1004.5132
  phi -0.0195929 0.08005300 0.0008005300 0.0025432838  990.7533

Quantiles:
         2.5%      25.0%     50.0%      75.0%      97.5%
   pi -0.332750 -0.2265245 -0.184088 -0.1285565 -0.0142326
   mu  1.353882  1.4111562  1.441424  1.4740774  1.5345210
equiv  1.000000  1.0000000  1.000000  1.0000000  1.0000000
 s2_2  0.001568  0.0061461  0.016302  0.0273322  0.0530448
 s2_1  0.001035  0.0043785  0.013677  0.0242892  0.0507633
theta  0.838904  0.9336518  0.974953  1.0320046  1.1567524
  phi -0.175659 -0.0686517 -0.025366  0.0315031  0.1456164