Eyes: Normal Mixture Model¶
An example from OpenBUGS [38], Bowmaker [6], and Robert [62] concerning 48 peak sensitivity wavelength measurements taken on a set of monkey’s eyes.
Analysis Program¶
using Mamba
## Data
eyes = [
:y =>
[529.0, 530.0, 532.0, 533.1, 533.4, 533.6, 533.7, 534.1, 534.8, 535.3,
535.4, 535.9, 536.1, 536.3, 536.4, 536.6, 537.0, 537.4, 537.5, 538.3,
538.5, 538.6, 539.4, 539.6, 540.4, 540.8, 542.0, 542.8, 543.0, 543.5,
543.8, 543.9, 545.3, 546.2, 548.8, 548.7, 548.9, 549.0, 549.4, 549.9,
550.6, 551.2, 551.4, 551.5, 551.6, 552.8, 552.9, 553.2],
:N => 48,
:alpha => [1, 1]
]
## Model Specification
model = Model(
y = Stochastic(1,
@modelexpr(lambda, T, s2, N,
begin
sigma = sqrt(s2)
Distribution[
begin
mu = lambda[T[i]]
Normal(mu, sigma)
end
for i in 1:N
]
end
),
false
),
T = Stochastic(1,
@modelexpr(p, N,
begin
P = Float64[p, 1 - p]
Distribution[Categorical(P) for i in 1:N]
end
),
false
),
p = Stochastic(
:(Uniform(0, 1))
),
lambda = Logical(1,
@modelexpr(lambda0, theta,
Float64[lambda0, lambda0 + theta]
)
),
lambda0 = Stochastic(
:(Normal(0.0, 1000.0)),
false
),
theta = Stochastic(
:(Uniform(0.0, 1000.0)),
false
),
s2 = Stochastic(
:(InverseGamma(0.001, 0.001))
)
)
## Initial Values
inits = [
[:y => eyes[:y], :T => fill(1, eyes[:N]), :p => 0.5, :lambda0 => 535,
:theta => 5, :s2 => 10],
[:y => eyes[:y], :T => fill(1, eyes[:N]), :p => 0.5, :lambda0 => 550,
:theta => 1, :s2 => 1]
]
## Sampling Scheme
scheme = [DGS([:T]),
Slice([:p, :lambda0, :theta, :s2], fill(1.0, 4), :univar, transform=true)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, eyes, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
lambda[1] 536.81290 0.9883483 0.011412463 0.052323509 356.8012
lambda[2] 548.75963 1.4660892 0.016928940 0.061653235 565.4693
p 0.59646 0.0909798 0.001050544 0.003005307 916.4579
s2 15.37891 7.1915331 0.083040671 0.406764080 312.5775
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
lambda[1] 535.086 536.17470 536.75185 537.36318 538.9397
lambda[2] 545.199 548.07943 548.86953 549.63026 551.1739
p 0.413 0.54206 0.60080 0.65619 0.7602
s2 8.637 11.40687 13.68101 16.78394 39.0676

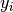 is the measurement on monkey
is the measurement on monkey 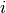 .
.