Leuk: Cox Regression¶

An example from OpenBUGS [38] and Ezzet and Whitehead [23] concerning survival in 42 leukemia patients treated with 6-mercaptopurine or placebo.

Model¶

Times to death are modelled using the Bayesian Cox proportional hazards model, formulated by Clayton [15] as

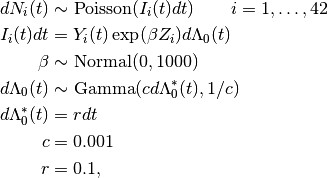
$dN_i(t) &\sim \text{Poisson}(I_i(t) dt) \quad\quad i=1,\ldots,42 \\ I_i(t)dt &= Y_i(t) \exp(\beta Z_i) d\Lambda_0(t) \\ \beta &\sim \text{Normal}(0, 1000) \\ d\Lambda_0(t) &\sim \text{Gamma}(c d\Lambda_0^*(t), 1 / c) \\ d\Lambda_0^*(t) &= r dt \\ c &= 0.001 \\ r &= 0.1,$

where 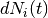$dN_i(t)$ is a counting process increment in time interval 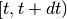$[t, t + dt)$ for patient 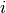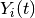$i$ ; $Y_i(t)$ is an indicator of whether the patient is observed at time 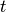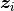$t$ ; $\bm{z}_i$ is a vector of covariates; and 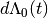$d\Lambda_0(t)$ is the increment in the integrated baseline hazard function during $[t, t + dt)$ .

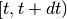Analysis Program¶

using Mamba

## Data
leuk = (Symbol => Any)[
  :t_obs =>
    [1, 1, 2, 2, 3, 4, 4, 5, 5, 8, 8, 8, 8, 11, 11, 12, 12, 15, 17, 22, 23, 6,
     6, 6, 6, 7, 9, 10, 10, 11, 13, 16, 17, 19, 20, 22, 23, 25, 32, 32, 34, 35],
  :fail =>
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0,
     1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
  :Z =>
    [0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
     0.5, 0.5, 0.5, 0.5, 0.5, 0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5,
     -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5,
     -0.5, -0.5],
  :t => [1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 22, 23, 35]
]
leuk[:N] = N = length(leuk[:t_obs])
leuk[:T] = T = length(leuk[:t]) - 1

leuk[:Y] = Array(Integer, N, T)
leuk[:dN] = Array(Integer, N, T)
for i in 1:N
  for j in 1:T
    leuk[:dN][i,j] = leuk[:fail][i] * (leuk[:t_obs][i] == leuk[:t][j])
    leuk[:Y][i,j] = int(leuk[:t_obs][i] >= leuk[:t][j])
  end
end

leuk[:c] = 0.001
leuk[:r] = 0.1


## Model Specification

model = Model(

  dN = Stochastic(2,
    @modelexpr(Y, beta, Z, dL0, N, T,
      Distribution[
        Y[i,j] > 0 ? Poisson(exp(beta * Z[i]) * dL0[j]) : Flat()
        for i in 1:N, j in 1:T
      ]
    ),
    false
  ),

  mu = Logical(1,
    @modelexpr(c, r, t,
      c * r * (t[2:end] - t[1:end-1])
    ),
    false
  ),

  dL0 = Stochastic(1,
    @modelexpr(mu, c, T,
      Distribution[Gamma(mu[j], 1 / c) for j in 1:T]
    ),
    false
  ),

  beta = Stochastic(
    :(Normal(0, 1000))
  ),

  S0 = Logical(1,
    @modelexpr(dL0,
      exp(-cumsum(dL0))
    ),
    false
  ),

  S_treat = Logical(1,
    @modelexpr(S0, beta,
      S0.^exp(-0.5 * beta)
    )
  ),

  S_placebo = Logical(1,
    @modelexpr(S0, beta,
      S0.^exp(0.5 * beta)
    )
  )

)


## Initial Values
inits = [
  [:dN => leuk[:dN], :beta => 0, :dL0 => fill(1, leuk[:T])],
  [:dN => leuk[:dN], :beta => 1, :dL0 => fill(2, leuk[:T])]
]


## Sampling Scheme
scheme = [AMWG([:dL0], fill(0.1, leuk[:T])),
          Slice([:beta], [3.0])]
setsamplers!(model, scheme)


## MCMC Simulations
sim = mcmc(model, leuk, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)

Results¶

Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750

Empirical Posterior Estimates:
                 Mean         SD        Naive SE       MCSE        ESS
   S_treat[1] 0.98302184 0.014032858 0.00016203749 0.0006383128  483.3092
   S_treat[2] 0.96624643 0.020819923 0.00024040776 0.0007446993  781.6213
   S_treat[3] 0.95620713 0.024534430 0.00028329919 0.0009465788  671.7975
   S_treat[4] 0.93643295 0.031636973 0.00036531230 0.0013470515  551.5965
   S_treat[5] 0.91398224 0.037982886 0.00043858859 0.0015468336  602.9603
   S_treat[6] 0.87937232 0.047653044 0.00055024996 0.0019138759  619.9458
   S_treat[7] 0.86752882 0.051602796 0.00059585777 0.0021775423  561.5821
   S_treat[8] 0.82175096 0.064689997 0.00074697574 0.0026883215  579.0444
   S_treat[9] 0.80555769 0.068612901 0.00079227353 0.0028610945  575.1050
  S_treat[10] 0.77183154 0.076942474 0.00088845517 0.0032446983  562.3202
  S_treat[11] 0.73565702 0.085534730 0.00098766999 0.0037453183  521.5639
  S_treat[12] 0.71260021 0.089598298 0.00103459203 0.0035843383  624.8583
  S_treat[13] 0.69113536 0.094685927 0.00109333891 0.0039840537  564.8336
  S_treat[14] 0.66442349 0.098857036 0.00114150273 0.0043081307  526.5474
  S_treat[15] 0.63642300 0.102857125 0.00118769178 0.0044398707  536.6957
  S_treat[16] 0.56561600 0.112893079 0.00130357699 0.0049775555  514.4017
  S_treat[17] 0.47103433 0.120102602 0.00138682539 0.0051081652  552.8088
 S_placebo[1] 0.92778986 0.050170096 0.00057931437 0.0023131639  470.4106
 S_placebo[2] 0.85943183 0.067291385 0.00077701399 0.0022336707  907.5710
 S_placebo[3] 0.82080457 0.074342778 0.00085843646 0.0025543630  847.0564
 S_placebo[4] 0.74834420 0.085488930 0.00098714114 0.0032803421  679.1747
 S_placebo[5] 0.67108872 0.090818803 0.00104868521 0.0031480313  832.2877
 S_placebo[6] 0.56465561 0.097783399 0.00112910544 0.0033397837  857.2225
 S_placebo[7] 0.53217331 0.099628193 0.00115040728 0.0036366205  750.5308
 S_placebo[8] 0.41887442 0.097451300 0.00112527068 0.0033070732  868.3357
 S_placebo[9] 0.38321055 0.095687796 0.00110490749 0.0031667575  913.0267
S_placebo[10] 0.31712209 0.091201496 0.00105310416 0.0029020050  987.6603
S_placebo[11] 0.25673919 0.086400289 0.00099766461 0.0026927518 1029.5270
S_placebo[12] 0.22301415 0.082260904 0.00094986710 0.0021934098 1406.5249
S_placebo[13] 0.19554723 0.079430544 0.00091718492 0.0024666426 1036.9615
S_placebo[14] 0.16485544 0.074276591 0.00085767220 0.0025275203  863.6040
S_placebo[15] 0.13703275 0.068763778 0.00079401571 0.0024652242  778.0484
S_placebo[16] 0.08379600 0.054748991 0.00063218689 0.0020924163  684.6302
S_placebo[17] 0.04092034 0.037737842 0.00043575906 0.0013746671  753.6315
         beta 1.55206443 0.424977799 0.00490722093 0.0111217466 1460.1131

Quantiles:
                 2.5%       25.0%      50.0%       75.0%       97.5%
   S_treat[1] 0.94621416 0.97721126 0.986955387 0.992864719 0.998368771
   S_treat[2] 0.91509516 0.95573219 0.970764331 0.981528195 0.993124279
   S_treat[3] 0.89749932 0.94319490 0.960671242 0.974341293 0.989582052
   S_treat[4] 0.85990686 0.91902353 0.941699242 0.959578177 0.981962464
   S_treat[5] 0.82397551 0.89249914 0.919841738 0.941506275 0.971669638
   S_treat[6] 0.77387551 0.85077283 0.885177533 0.913944652 0.955211053
   S_treat[7] 0.75318224 0.83615928 0.873267366 0.904856224 0.950378212
   S_treat[8] 0.68017136 0.78096730 0.828861810 0.868789540 0.928833884
   S_treat[9] 0.65553285 0.76283692 0.813277192 0.854664506 0.919302649
  S_treat[10] 0.60268487 0.72360801 0.779448002 0.826762737 0.901699132
  S_treat[11] 0.55030830 0.68188164 0.743447395 0.797449392 0.879907216
  S_treat[12] 0.52335655 0.65497052 0.720927823 0.777608202 0.864661623
  S_treat[13] 0.49228689 0.63108504 0.699537585 0.758920006 0.852628141
  S_treat[14] 0.45972979 0.59839293 0.670665550 0.735415731 0.838250322
  S_treat[15] 0.42697507 0.56653713 0.641228870 0.709931594 0.822082952
  S_treat[16] 0.34387359 0.48788044 0.566936069 0.644918756 0.777491390
  S_treat[17] 0.24667350 0.38339560 0.469857377 0.555064846 0.702808815
 S_placebo[1] 0.79979042 0.90318503 0.939595572 0.964924422 0.990890790
 S_placebo[2] 0.70559587 0.81931331 0.869352795 0.908385797 0.963186970
 S_placebo[3] 0.65639888 0.77312423 0.828159645 0.876023887 0.943371309
 S_placebo[4] 0.56607932 0.69244455 0.754818343 0.810412223 0.894624799
 S_placebo[5] 0.48516052 0.60948198 0.675431460 0.736195314 0.836155269
 S_placebo[6] 0.36968729 0.49714945 0.566089714 0.632288659 0.749328787
 S_placebo[7] 0.34028564 0.46293915 0.532290556 0.601897323 0.724841278
 S_placebo[8] 0.23796143 0.34940586 0.415075601 0.483568964 0.620503275
 S_placebo[9] 0.20912939 0.31494786 0.378301304 0.447909630 0.582109553
S_placebo[10] 0.15624653 0.25026510 0.311673305 0.378896633 0.510893913
S_placebo[11] 0.10926572 0.19326201 0.249637651 0.312589668 0.443600588
S_placebo[12] 0.08456597 0.16203246 0.216266931 0.276356661 0.404484250
S_placebo[13] 0.06502276 0.13721863 0.187654643 0.246139543 0.373111561
S_placebo[14] 0.04794312 0.11042966 0.156032281 0.209723502 0.331684320
S_placebo[15] 0.03427845 0.08617175 0.127242826 0.176712122 0.295007629
S_placebo[16] 0.01255699 0.04295264 0.072131767 0.112032446 0.220466119
S_placebo[17] 0.00216784 0.01395971 0.029822826 0.055822282 0.140786390
         beta 0.75242446 1.25909288 1.540715015 1.829373993 2.418625723