Magnesium: Meta-Analysis Prior Sensitivity¶

An example from OpenBUGS [38].

Model¶

Number of events reported for treatment and control subjects in 8 studies is modelled as

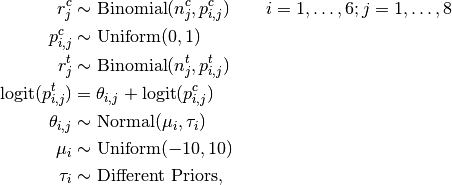
$r^c_j &\sim \text{Binomial}(n^c_j, p^c_{i,j}) \quad\quad i=1,\ldots,6; j=1,\ldots,8 \\ p^c_{i,j} &\sim \text{Uniform}(0, 1) \\ r^t_j &\sim \text{Binomial}(n^t_j, p^t_{i,j}) \\ \operatorname{logit}(p^t_{i,j}) &= \theta_{i,j} + \operatorname{logit}(p^c_{i,j}) \\ \theta_{i,j} &\sim \text{Normal}(\mu_i, \tau_i) \\ \mu_i &\sim \text{Uniform}(-10, 10) \\ \tau_i &\sim \text{Different Priors},$

where 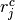$r^c_j$ is the number of control group events, out of 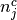$n^c_j$ , in study 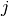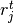$j$ ; $r^t_j$ is the number of treatment group events; and 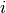$i$ indexes differ prior specifications.

Analysis Program¶

using Mamba

## Data
magnesium = (Symbol => Any)[
  :rt => [1, 9, 2, 1, 10, 1, 1, 90],
  :nt => [40, 135, 200, 48, 150, 59, 25, 1159],
  :rc => [2, 23, 7, 1, 8, 9, 3, 118],
  :nc => [36, 135, 200, 46, 148, 56, 23, 1157]
]

magnesium[:rtx] = hcat([magnesium[:rt] for i in 1:6]...)'
magnesium[:rcx] = hcat([magnesium[:rc] for i in 1:6]...)'
magnesium[:s2] = 1 ./ (magnesium[:rt] + 0.5) +
                 1 ./ (magnesium[:nt] - magnesium[:rt] + 0.5) +
                 1 ./ (magnesium[:rc] + 0.5) +
                 1 ./ (magnesium[:nc] - magnesium[:rc] + 0.5)
magnesium[:s2_0] = 1 / mean(1 ./ magnesium[:s2])


## Model Specification

model = Model(

  rcx = Stochastic(2,
    @modelexpr(nc, pc,
      Distribution[Binomial(nc[j], pc[i,j]) for i in 1:6, j in 1:8]
    ),
    false
  ),

  pc = Stochastic(2,
    :(Uniform(0, 1)),
    false
  ),

  rtx = Stochastic(2,
    @modelexpr(nt, pc, theta,
      Distribution[
        begin
          phi = logit(pc[i,j])
          pt = invlogit(theta[i,j] + phi)
          Binomial(nt[j], pt)
        end
        for i in 1:6, j in 1:8
      ]
    ),
    false
  ),

  theta = Stochastic(2,
    @modelexpr(mu, tau,
      Distribution[Normal(mu[i], tau[i]) for i in 1:6, j in 1:8]
    ),
    false
  ),

  mu = Stochastic(1,
    :(Uniform(-10, 10)),
    false
  ),

  OR = Logical(1,
    @modelexpr(mu,
      exp(mu)
    )
  ),

  tau = Logical(1,
    @modelexpr(priors, s2_0,
      [ sqrt(priors[1]),
        sqrt(priors[2]),
        priors[3],
        sqrt(s2_0 * (1 / priors[4] - 1)),
        sqrt(s2_0) * (1 / priors[5] - 1),
        sqrt(priors[6]) ]
    )
  ),

  priors = Stochastic(1,
    @modelexpr(s2_0,
      Distribution[
        InverseGamma(0.001, 0.001),
        Uniform(0, 50),
        Uniform(0, 50),
        Uniform(0, 1),
        Uniform(0, 1),
        Truncated(Normal(0, sqrt(s2_0 / erf(0.75))), 0, Inf)
      ]
    ),
    false
  )

)


## Initial Values
inits = [
  [:rcx => magnesium[:rcx], :rtx => magnesium[:rtx],
   :theta => zeros(6, 8), :mu => fill(-0.5, 6),
   :pc => fill(0.5, 6, 8), :priors => [1, 1, 1, 0.5, 0.5, 1]],
  [:rcx => magnesium[:rcx], :rtx => magnesium[:rtx],
   :theta => zeros(6, 8), :mu => fill(0.5, 6),
   :pc => fill(0.5, 6, 8), :priors => [1, 1, 1, 0.5, 0.5, 1]]
]


## Sampling Scheme
scheme = [AMWG([:theta], fill(0.1, 48)),
          AMWG([:mu], fill(0.1, 6)),
          Slice([:pc], fill(0.25, 48), :univar),
          Slice([:priors], [1.0, 5.0, 5.0, 0.25, 0.25, 5.0], :univar)]
setsamplers!(model, scheme)


## MCMC Simulations
sim = mcmc(model, magnesium, inits, 12500, burnin=2500, thin=2, chains=2)
describe(sim)

Results¶

Iterations = 2502:12500
Thinning interval = 2
Chains = 1,2
Samples per chain = 5000

Empirical Posterior Estimates:
          Mean       SD       Naive SE      MCSE       ESS
 OR[1] 0.4938813 0.16724218 0.001672422 0.006780965  608.2872
 OR[2] 0.4693250 1.10491202 0.011049120 0.030148804 1343.1213
 OR[3] 0.4449415 0.21477655 0.002147765 0.005421447 1569.4347
 OR[4] 0.4749598 0.13873544 0.001387354 0.005962572  541.3866
 OR[5] 0.4936191 0.15045871 0.001504587 0.006343458  562.5778
 OR[6] 0.4452843 0.14497511 0.001449751 0.005554683  681.1902
tau[1] 0.5005081 0.38002286 0.003800229 0.019431081  382.4948
tau[2] 1.1646043 0.75346006 0.007534601 0.037904158  395.1362
tau[3] 0.8082610 0.49226340 0.004922634 0.018663493  695.6796
tau[4] 0.4676924 0.27044423 0.002704442 0.011446738  558.2027
tau[5] 0.4523501 0.34711372 0.003471137 0.017258471  404.5190
tau[6] 0.5734504 0.19406724 0.001940672 0.006299041  949.1953

Quantiles:
          2.5%       25.0%      50.0%      75.0%     97.5%
 OR[1] 0.20905560 0.38255153 0.48785122 0.59332617 0.8138231
 OR[2] 0.11223358 0.27027567 0.38254203 0.51449190 1.0372736
 OR[3] 0.15915375 0.31983172 0.42081185 0.53465139 0.8806431
 OR[4] 0.21563818 0.38285241 0.47223709 0.56044575 0.7647249
 OR[5] 0.20841340 0.38723776 0.49357081 0.60852910 0.7656372
 OR[6] 0.21100558 0.34464323 0.42943747 0.52740053 0.7759471
tau[1] 0.03672526 0.20687073 0.43248769 0.69829673 1.4601677
tau[2] 0.29554286 0.68477332 0.98359802 1.40115062 3.3037132
tau[3] 0.13105672 0.48296429 0.71422501 1.02092799 2.0156086
tau[4] 0.07837793 0.28460737 0.41764937 0.59299427 1.1350358
tau[5] 0.02041302 0.18367182 0.39716777 0.63507897 1.2857608
tau[6] 0.20363568 0.43899364 0.57124610 0.70377109 0.9609324