Mice: Weibull Regression¶
An example from OpenBUGS [38], Grieve [37], and Dellaportas and Smith [19] concerning time to death or censoring among four groups of 20 mice each.
Model¶
Time to events are modelled as
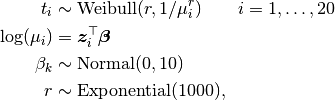
where 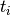 is the time of death for mouse
is the time of death for mouse 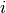 , and
, and 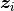 is a vector of covariates.
is a vector of covariates.
Analysis Program¶
using Mamba
## Data
mice = (Symbol => Any)[
:t =>
[12 1 21 25 11 26 27 30 13 12 21 20 23 25 23 29 35 NaN 31 36
32 27 23 12 18 NaN NaN 38 29 30 NaN 32 NaN NaN NaN NaN 25 30 37 27
22 26 NaN 28 19 15 12 35 35 10 22 18 NaN 12 NaN NaN 31 24 37 29
27 18 22 13 18 29 28 NaN 16 22 26 19 NaN NaN 17 28 26 12 17 26],
:tcensor =>
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 40 0 0
0 0 0 0 0 40 40 0 0 0 40 0 40 40 40 40 0 0 0 0
0 0 10 0 0 0 0 0 0 0 0 0 24 0 40 40 0 0 0 0
0 0 0 0 0 0 0 20 0 0 0 0 29 10 0 0 0 0 0 0]
]
mice[:M] = size(mice[:t], 1)
mice[:N] = size(mice[:t], 2)
## Model Specification
model = Model(
t = Stochastic(2,
@modelexpr(r, beta, tcensor, M, N,
Distribution[
begin
lambda = exp(-beta[i] / r)
0 < lambda < Inf ?
Truncated(Weibull(r, lambda), tcensor[i,j], Inf) :
Uniform(0, Inf)
end
for i in 1:M, j in 1:N
]
),
false
),
r = Stochastic(
:(Exponential(1000))
),
beta = Stochastic(1,
:(Normal(0, 10)),
false
),
median = Logical(1,
@modelexpr(beta, r,
exp(-beta / r) * log(2)^(1/r)
)
),
veh_control = Logical(
@modelexpr(beta,
beta[2] - beta[1]
)
),
test_sub = Logical(
@modelexpr(beta,
beta[3] - beta[1]
)
),
pos_control = Logical(
@modelexpr(beta,
beta[4] - beta[1]
)
)
)
## Initial Values
inits = [
[:t => mice[:t], :beta => fill(-1, mice[:M]), :r => 1.0],
[:t => mice[:t], :beta => fill(-2, mice[:M]), :r => 1.0]
]
## Sampling Scheme
scheme = [MISS([:t]),
Slice([:beta], fill(1.0, mice[:M]), :univar),
Slice([:r], [0.25])]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, mice, inits, 20000, burnin=2500, thin=2, chains=2)
describe(sim)