Seeds: Random Effect Logistic Regression¶
An example from OpenBUGS [38], Crowder [17], and Breslow and Clayton [9] concerning the proportion of seeds that germinated on each of 21 plates arranged according to a 2 by 2 factorial layout by seed and type of root extract.
Model¶
Germinations are modelled as

where 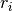 are the number of seeds, out of
are the number of seeds, out of 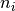 , that germinate on plate
, that germinate on plate 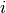 ; and
; and 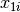 and
and 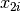 are the seed type and root extract.
are the seed type and root extract.
Analysis Program¶
using Mamba
## Data
seeds = (Symbol => Any)[
:r => [10, 23, 23, 26, 17, 5, 53, 55, 32, 46, 10, 8, 10, 8, 23, 0, 3, 22, 15,
32, 3],
:n => [39, 62, 81, 51, 39, 6, 74, 72, 51, 79, 13, 16, 30, 28, 45, 4, 12, 41,
30, 51, 7],
:x1 => [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
:x2 => [0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
]
seeds[:N] = length(seeds[:r])
## Model Specification
model = Model(
r = Stochastic(1,
@modelexpr(alpha0, alpha1, x1, alpha2, x2, alpha12, b, n, N,
Distribution[
begin
p = invlogit(alpha0 + alpha1 * x1[i] + alpha2 * x2[i] +
alpha12 * x1[i] * x2[i] + b[i])
Binomial(n[i], p)
end
for i in 1:N
]
),
false
),
b = Stochastic(1,
@modelexpr(s2,
Normal(0, sqrt(s2))
),
false
),
alpha0 = Stochastic(
:(Normal(0, 1000))
),
alpha1 = Stochastic(
:(Normal(0, 1000))
),
alpha2 = Stochastic(
:(Normal(0, 1000))
),
alpha12 = Stochastic(
:(Normal(0, 1000))
),
s2 = Stochastic(
:(InverseGamma(0.001, 0.001))
)
)
## Initial Values
inits = [
[:r => seeds[:r], :alpha0 => 0, :alpha1 => 0, :alpha2 => 0,
:alpha12 => 0, :s2 => 0.01, :b => zeros(seeds[:N])],
[:r => seeds[:r], :alpha0 => 0, :alpha1 => 0, :alpha2 => 0,
:alpha12 => 0, :s2 => 1, :b => zeros(seeds[:N])]
]
## Sampling Scheme
scheme = [AMM([:alpha0, :alpha1, :alpha2, :alpha12], 0.01 * eye(4)),
AMWG([:b], fill(0.01, seeds[:N])),
AMWG([:s2], [0.1])]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, seeds, inits, 12500, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:12500
Thinning interval = 2
Chains = 1,2
Samples per chain = 5000
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
alpha2 1.3107281 0.26053104 0.0026053104 0.016391301 252.63418
s2 0.0857053 0.09738014 0.0009738014 0.008167153 142.16720
alpha0 -0.5561543 0.17595432 0.0017595432 0.011366011 239.65346
alpha12 -0.7464409 0.43006756 0.0043006756 0.026796428 257.58440
alpha1 0.0887002 0.26872879 0.0026872879 0.013771345 380.78132
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
alpha2 0.80405938 1.1488818 1.3099477 1.4807632 1.8281561
s2 0.00117398 0.0211176 0.0593763 0.1114008 0.3523464
alpha0 -0.91491978 -0.6666323 -0.5512929 -0.4426242 -0.2224477
alpha12 -1.54570414 -1.0275765 -0.7572503 -0.4914919 0.1702970
alpha1 -0.42501648 -0.0936379 0.0943906 0.2600758 0.6235393