Stacks: Robust Regression¶
An example from OpenBUGS [38], Brownlee [12], and Birkes and Dodge [4] concerning 21 daily responses of stack loss, the amount of ammonia escaping, as a function of air flow, temperature, and acid concentration.
Analysis Program¶
using Mamba
## Data
stacks = (Symbol => Any)[
:y => [42, 37, 37, 28, 18, 18, 19, 20, 15, 14, 14, 13, 11, 12, 8, 7, 8, 8, 9,
15, 15],
:x =>
[80 27 89
80 27 88
75 25 90
62 24 87
62 22 87
62 23 87
62 24 93
62 24 93
58 23 87
58 18 80
58 18 89
58 17 88
58 18 82
58 19 93
50 18 89
50 18 86
50 19 72
50 19 79
50 20 80
56 20 82
70 20 91]
]
stacks[:N] = size(stacks[:x], 1)
stacks[:p] = size(stacks[:x], 2)
stacks[:meanx] = map(j -> mean(stacks[:x][:,j]), 1:stacks[:p])
stacks[:sdx] = map(j -> std(stacks[:x][:,j]), 1:stacks[:p])
stacks[:z] = Float64[
(stacks[:x][i,j] - stacks[:meanx][j]) / stacks[:sdx][j]
for i in 1:stacks[:N], j in 1:stacks[:p]
]
## Model Specification
model = Model(
y = Stochastic(1,
@modelexpr(mu, s2, N,
begin
Distribution[Laplace(mu[i], s2) for i in 1:N]
end
),
false
),
beta0 = Stochastic(
:(Normal(0, 1000)),
false
),
beta = Stochastic(1,
:(Normal(0, 1000)),
false
),
mu = Logical(1,
@modelexpr(beta0, z, beta,
beta0 + z * beta
),
false
),
s2 = Stochastic(
:(InverseGamma(0.001, 0.001)),
false
),
sigma = Logical(
@modelexpr(s2,
sqrt(2.0) * s2
)
),
b0 = Logical(
@modelexpr(beta0, b, meanx,
beta0 - dot(b, meanx)
)
),
b = Logical(1,
@modelexpr(beta, sdx,
beta ./ sdx
)
),
outlier = Logical(1,
@modelexpr(y, mu, sigma, N,
Float64[abs((y[i] - mu[i]) / sigma) > 2.5 for i in 1:N]
),
[1,3,4,21]
)
)
## Initial Values
inits = [
[:y => stacks[:y], :beta0 => 10, :beta => [0, 0, 0], :s2 => 10],
[:y => stacks[:y], :beta0 => 1, :beta => [1, 1, 1], :s2 => 1]
]
## Sampling Scheme
scheme = [NUTS([:beta0, :beta]),
Slice([:s2], [1.0])]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, stacks, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
b[1] 0.83445 0.1297656 0.001498404 0.00227082 3265.534
b[2] 0.75151 0.3329099 0.003844112 0.00562761 3499.489
b[3] -0.11714 0.1196021 0.001381046 0.00160727 5537.350
outlier[1] 0.03893 0.1934490 0.002233757 0.00285110 4603.713
outlier[3] 0.05587 0.2296794 0.002652109 0.00357717 4122.536
outlier[4] 0.30000 0.4582881 0.005291855 0.00861175 2832.010
outlier[21] 0.60987 0.4878125 0.005632774 0.01106491 1943.615
b0 -38.73747 8.6797300 0.100224890 0.10329322 7061.042
sigma 3.46651 0.8548797 0.009871301 0.02758864 960.173
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
b[1] 0.568641 0.754152 0.835908 0.916990 1.089509
b[2] 0.178021 0.525812 0.723047 0.947780 1.480699
b[3] -0.366040 -0.189466 -0.112007 -0.041001 0.111335
outlier[1] 0.000000 0.000000 0.000000 0.000000 1.000000
outlier[3] 0.000000 0.000000 0.000000 0.000000 1.000000
outlier[4] 0.000000 0.000000 0.000000 1.000000 1.000000
outlier[21] 0.000000 0.000000 1.000000 1.000000 1.000000
b0 -56.503611 -44.046775 -38.745722 -33.417515 -21.737427
sigma 2.177428 2.860547 3.337315 3.941882 5.509634
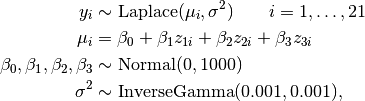
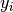 is the stack loss on day
is the stack loss on day 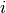 ; and
; and 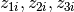 are standardized predictors.
are standardized predictors.