Distributions¶

Given in this section are distributions, as provided by the Distributions [1] and Mamba packages, supported for the specification of Stochastic nodes. Truncated versions of continuous univariate distributions are also supported.

Univariate Distributions¶

Distributions Package Univariate Types¶

The following univariate types from the Distributions package are supported.

Arcsine       Cosine            Hypergeometric    NegativeBinomial   Rayleigh
Bernoulli     DiscreteUniform   InverseGamma      NoncentralBeta     Skellam
Beta          Edgeworth         InverseGaussian   NoncentralChisq    TDist
BetaPrime     Erlang            KSDist            NoncentralF        TriangularDist
Binomial      Exponential       KSOneSided        NoncentralT        Uniform
Categorical   FDist             Laplace           Normal             Weibull
Cauchy        Gamma             Levy              NormalCanon
Chi           Geometric         Logistic          Pareto
Chisq         Gumbel            LogNormal         Poisson

Flat Distribution¶

A Flat distribution is supplied with the degenerate probability density function:

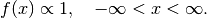
$f(x) \propto 1, \quad -\infty < x < \infty.$

Flat()    # Flat distribution

User-Defined Univariate Distributions¶

New known, unknown, or unnormalized univariate distributions can be created and added to Mamba as subtypes of the Distributions package ContinuousUnivariateDistribution or DiscreteUnivariateDistribution types. Mamba requires only a partial implementation of the method functions described in the full instructions for creating univariate distributions. The specific workflow is given below.

Create a quote block for the new distribution. Assign the block a variable name, say extensions, preceded by the @everywhere macro to ensure compatibility when julia is run in multi-processor mode.

The Distributions package contains types and method definitions for new distributions. Load the package and import the package’s methods (indicated below) to be extended.

Declare a new distribution subtype, say D, within the block. Create a constructor for the subtype that accepts un-typed arguments and explicitly converts them in the constructor body to the proper types for the fields of D. Implementing the constructor in this way ensures that it will be callable with the Mamba Stochastic and Logical types.

Extend/define the following Distributions package methods for the new distribution D.

minimum(d::D)¶

Return the lower bound of the support of d.

maximum(d::D)¶

Return the upper bound of the support of d.

logpdf(d::D, x::Real)¶

Return the normalized or unnomalized log-density evaluated at x.

Test the subtype.
Add the quote block (new distribution) to Mamba with the following calls.
using Mamba
@everywhere eval(Mamba, extensions)

Below is a univariate example based on the linear regression model in the Tutorial.

## Define a new univariate Distribution type for Mamba.
## The definition must be placed within an unevaluated quote block.
@everywhere extensions = quote

  ## Load needed packages and import methods to be extended
  using Distributions
  import Distributions: minimum, maximum, logpdf

  ## Type declaration
  type NewUnivarDist <: ContinuousUnivariateDistribution
    mu::Float64
    sigma::Float64

    ## Constructor
    function NewUnivarDist(mu, sigma)
      new(convert(Float64, mu), convert(Float64, sigma))
    end
  end

  ## The following method functions must be implemented

  ## Minimum and maximum support values
  minimum(d::NewUnivarDist) = -Inf
  maximum(d::NewUnivarDist) = Inf

  ## Normalized or unnormalized log-density value
  function logpdf(d::NewUnivarDist, x::Real)
    -log(d.sigma) - 0.5 * ((x - d.mu) / d.sigma)^2
  end

end

## Test the extensions in a temporary module (optional)
module Testing end
eval(Testing, extensions)
d = Testing.NewUnivarDist(0.0, 1.0)
Testing.minimum(d)
Testing.maximum(d)
Testing.insupport(d, 2.0)
Testing.logpdf(d, 2.0)

## Add the extensions to Mamba
using Mamba
@everywhere eval(Mamba, extensions)

## Implement a Mamba model using the new distribution
model = Model(

  y = Stochastic(1,
    @modelexpr(mu, s2,
      begin
        sigma = sqrt(s2)
        Distribution[NewUnivarDist(mu[i], sigma) for i in 1:length(mu)]
      end
    ),
    false
  ),

  mu = Logical(1,
    @modelexpr(xmat, beta,
      xmat * beta
    ),
    false
  ),

  beta = Stochastic(1,
    :(MvNormal(2, sqrt(1000)))
  ),

  s2 = Stochastic(
    :(InverseGamma(0.001, 0.001))
  )

)

## Sampling Scheme
scheme = [NUTS([:beta]),
          Slice([:s2], [3.0])]

## Sampling Scheme Assignment
setsamplers!(model, scheme)

## Data
line = (Symbol => Any)[
  :x => [1, 2, 3, 4, 5],
  :y => [1, 3, 3, 3, 5]
]
line[:xmat] = [ones(5) line[:x]]

## Initial Values
inits = Dict{Symbol,Any}[
  [:y => line[:y],
   :beta => rand(Normal(0, 1), 2),
   :s2 => rand(Gamma(1, 1))]
  for i in 1:3]

## MCMC Simulation
sim = mcmc(model, line, inits, 10000, burnin=250, thin=2, chains=3)
describe(sim)

Multivariate Distributions¶

Distributions Package Multivariate Types¶

The following multivariate types from the Distributions package are supported.

Dirichlet    Multinomial     MvNormal          MvNormalCannon
MvTDist      VonMisesFisher

Block-Diagonal Multivariate Normal Distribution¶

A Block-Diagonal Multivariate Normal distribution is supplied with the probability density function:

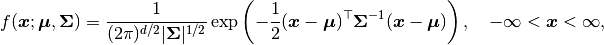
$f(\bm{x}; \bm{\mu}, \bm{\Sigma}) = \frac{1}{(2 \pi)^{d/2} |\bm{\Sigma}|^{1/2}} \exp\left(-\frac{1}{2} (\bm{x} - \bm{\mu})^\top \bm{\Sigma}^{-1} (\bm{x} - \bm{\mu})\right), \quad -\infty < \bm{x} < \infty,$

where

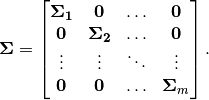
$\bm{\Sigma} = \begin{bmatrix} \bm{\Sigma_1} & \bm{0} & \hdots & \bm{0} \\ \bm{0} & \bm{\Sigma_2} & \hdots & \bm{0} \\ \vdots & \vdots & \ddots & \vdots \\ \bm{0} & \bm{0} & \hdots & \bm{\Sigma}_m \\ \end{bmatrix}.$

BDiagNormal(mu, C)    # multivariate normal with mean vector mu and block-
                      # diagonal covariance matrix Sigma such that
                      # length(mu) = dim(Sigma), and Sigma_1 = ... = Sigma_m = C
                      # for a matrix C or Sigma_1 = C[1], ..., Sigma_m = C[m]
                      # for a vector of matrices C.

User-Defined Multivariate Distributions¶

New known, unknown, or unnormalized multivariate distributions can be created and added to Mamba as subtypes of the Distributions package ContinuousMultivariateDistribution or DiscreteMultivariateDistribution types. Mamba requires only a partial implementation of the method functions described in the full instructions for creating multivariate distributions. The specific workflow is given below.

Create a quote block for the new distribution. Assign the block a variable name, say extensions, preceded by the @everywhere macro to ensure compatibility when julia is run in multi-processor mode.

The Distributions package contains types and method definitions for new distributions. Load the package and import the package’s methods (indicated below) to be extended.

Declare a new distribution subtype, say D, within the block. Create a constructor for the subtype that accepts un-typed arguments and explicitly converts them in the constructor body to the proper types for the fields of D. Implementing the constructor in this way ensures that it will be callable with the Mamba Stochastic and Logical types.

Extend/define the following Distributions package methods for the new distribution D.

length(d::D)¶

Return the sample space size (dimension) of d.

insupport{T<:Real}(d::D, x::Vector{T})¶

Return a logical indicating whether x is in the support of d.

_logpdf{T<:Real}(d::D, x::Vector{T})¶

Return the normalized or unnomalized log-density evaluated at x.

Test the subtype.
Add the quote block (new distribution) to Mamba with the following calls.
using Mamba
@everywhere eval(Mamba, extensions)

Below is a multivariate example based on the linear regression model in the Tutorial.

## Define a new multivariate Distribution type for Mamba.
## The definition must be placed within an unevaluated quote block.
@everywhere extensions = quote

  ## Load needed packages and import methods to be extended
  using Distributions
  import Distributions: length, insupport, _logpdf

  ## Type declaration
  type NewMultivarDist <: ContinuousMultivariateDistribution
    mu::Vector{Float64}
    sigma::Float64

    ## Constructor
    function NewMultivarDist(mu, sigma)
      new(convert(Vector{Float64}, mu), convert(Float64, sigma))
    end
  end

  ## The following method functions must be implemented

  ## Dimension of the distribution
  length(d::NewMultivarDist) = length(d.mu)

  ## Logicals indicating whether elements of x are in the support
  function insupport{T<:Real}(d::NewMultivarDist, x::Vector{T})
    length(d) == length(x) && all(isfinite(x))
  end

  ## Normalized or unnormalized log-density value
  function _logpdf{T<:Real}(d::NewMultivarDist, x::Vector{T})
    -length(x) * log(d.sigma) - 0.5 * sumabs2(x - d.mu) / d.sigma^2
  end

end

## Test the extensions in a temporary module (optional)
module Testing end
eval(Testing, extensions)
d = Testing.NewMultivarDist([0.0, 0.0], 1.0)
Testing.insupport(d, [2.0, 3.0])
Testing.logpdf(d, [2.0, 3.0])

## Add the extensions to Mamba
using Mamba
@everywhere eval(Mamba, extensions)

## Implement a Mamba model using the new distribution
model = Model(

  y = Stochastic(1,
    @modelexpr(mu, s2,
      NewMultivarDist(mu, sqrt(s2))
    ),
    false
  ),

  mu = Logical(1,
    @modelexpr(xmat, beta,
      xmat * beta
    ),
    false
  ),

  beta = Stochastic(1,
    :(MvNormal(2, sqrt(1000)))
  ),

  s2 = Stochastic(
    :(InverseGamma(0.001, 0.001))
  )

)

## Sampling Scheme
scheme = [NUTS([:beta]),
          Slice([:s2], [3.0])]

## Sampling Scheme Assignment
setsamplers!(model, scheme)

## Data
line = (Symbol => Any)[
  :x => [1, 2, 3, 4, 5],
  :y => [1, 3, 3, 3, 5]
]
line[:xmat] = [ones(5) line[:x]]

## Initial Values
inits = Dict{Symbol,Any}[
  [:y => line[:y],
   :beta => rand(Normal(0, 1), 2),
   :s2 => rand(Gamma(1, 1))]
  for i in 1:3]

## MCMC Simulation
sim = mcmc(model, line, inits, 10000, burnin=250, thin=2, chains=3)
describe(sim)

Matrix-Variate Distributions¶

Distributions Package Matrix-Variate Types¶

The following matrix-variate types from the Distributions package are supported.

InverseWishart   Wishart