No-U-Turn Sampler (NUTS)¶

Implementation of the NUTS extension (algorithm 6) [42] to Hamiltonian Monte Carlo [53] for simulating autocorrelated draws from a distribution that can be specified up to a constant of proportionality.

Stand-Alone Functions¶

nutsepsilon(v::NUTSVariate, fx::Function)¶

Generate an initial value for the step size parameter of the No-U-Turn sampler. Parameters are assumed to be continuous and unconstrained.

Arguments

v : the current state of parameters to be simulated.

fx : function to compute the log-transformed density (up to a normalizing constant) and gradient vector at v.value, and to return the respective results as a tuple.

Value

A numeric step size value.

nuts!(v::NUTSVariate, epsilon::Real, fx::Function; adapt::Bool=false, target::Real=0.6)¶

Simulate one draw from a target distribution using the No-U-Turn sampler. Parameters are assumed to be continuous and unconstrained.

Arguments

v : current state of parameters to be simulated. When running the sampler in adaptive mode, the v argument in a successive call to the function should contain the tune field returned by the previous call.

epsilon : the NUTS algorithm step size parameter.

fx : function to compute the log-transformed density (up to a normalizing constant) and gradient vector at v.value, and to return the respective results as a tuple.

adapt : whether to adaptively update the epsilon step size parameter.

target : a target acceptance rate for the algorithm.

Value

Returns v updated with simulated values and associated tuning parameters.

Example

The following example samples parameters in a simple linear regression model. Details of the model specification and posterior distribution can be found in the Supplement.

################################################################################
## Linear Regression
##   y ~ N(b0 + b1 * x, s2)
##   b0, b1 ~ N(0, 1000)
##   s2 ~ invgamma(0.001, 0.001)
################################################################################

using Mamba

## Data
data = [
  :x => [1, 2, 3, 4, 5],
  :y => [1, 3, 3, 3, 5]
]

## Log-transformed Posterior(b0, b1, log(s2)) + Constant and Gradient Vector
fx = function(x)
  b0 = x[1]
  b1 = x[2]
  logs2 = x[3]
  r = data[:y] - b0 - b1 * data[:x]
  logf = (-0.5 * length(data[:y]) - 0.001) * logs2 -
           (0.5 * dot(r, r) + 0.001) / exp(logs2) -
           0.5 * b0^2 / 1000 - 0.5 * b1^2 / 1000
  grad = [
    sum(r) / exp(logs2) - b0 / 1000,
    sum(data[:x] .* r) / exp(logs2) - b1 / 1000,
    -0.5 * length(data[:y]) - 0.001 + (0.5 * dot(r, r) + 0.001) / exp(logs2)
  ]
  logf, grad
end

## MCMC Simulation with No-U-Turn Sampling
n = 5000
burnin = 1000
sim = Chains(n, 3, start = (burnin + 1), names = ["b0", "b1", "s2"])
theta = NUTSVariate([0.0, 0.0, 0.0])
epsilon = nutsepsilon(theta, fx)
for i in 1:n
  nuts!(theta, epsilon, fx, adapt = (i <= burnin))
  if i > burnin
    sim[i,:,1] = [theta[1:2], exp(theta[3])]
  end
end
describe(sim)

NUTSVariate Type¶

Declaration¶

NUTSVariate <: VectorVariate

Fields¶

value::Vector{VariateType} : vector of sampled values.
tune::NUTSTune : tuning parameters for the sampling algorithm.

Constructors¶

NUTSVariate(x::Vector{VariateType}, tune::NUTSTune)¶

NUTSVariate(x::Vector{VariateType}, tune=nothing)

Construct a NUTSVariate object that stores sampled values and tuning parameters for No-U-Turn sampling.

Arguments

x : vector of sampled values.

tune : tuning parameters for the sampling algorithm. If nothing is supplied, parameters are set to their defaults.

Value

Returns a NUTSVariate type object with fields pointing to the values supplied to arguments x and tune.

NUTSTune Type¶

Declaration¶

type NUTSTune

Fields¶

adapt::Bool : whether the proposal distribution has been adaptively tuned.
alpha::Float64 : cumulative acceptance probabilities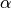 $\alpha$ from leapfrog steps.
epsilon::Float64 : updated value of the step size parameter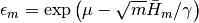 $\epsilon_m = \exp\left(\mu - \sqrt{m} \bar{H}_m / \gamma\right)$ if adapt = true, and the user-defined value otherwise.
epsbar::Float64 : dual averaging parameter, defined as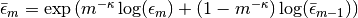 $\bar{\epsilon}_m = \exp\left(m^{-\kappa} \log(\epsilon_m) + (1 - m^{-\kappa}) \log(\bar{\epsilon}_{m-1})\right)$ .
gamma::Float64 : dual averaging parameter, fixed at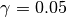 $\gamma = 0.05$ .
Hbar::Float64 : dual averaging parameter, defied as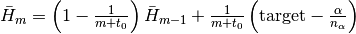 $\bar{H}_m = \left(1 - \frac{1}{m + t_0}\right) \bar{H}_{m-1} + \frac{1}{m + t_0} \left(\text{target} - \frac{\alpha}{n_\alpha}\right)$ .
kappa::Float64 : dual averaging parameter, fixed at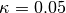 $\kappa = 0.05$ .
m::Integer : number of adaptive update iterations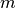 $m$ that have been performed.
mu::Float64 : dual averaging parameter, defined as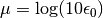 $\mu = \log(10 \epsilon_0)$ .
nalpha::Integer : the total number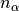 $n_\alpha$ of leapfrog steps performed.
t0::Float64 : dual averaging parameter, fixed at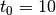 $t_0 = 10$ .
target::Float64 : target acceptance rate for the adaptive algorithm.

Sampler Constructor¶

NUTS(params::Vector{Symbol}; dtype::Symbol=:forward, target::Real=0.6)¶

Construct a Sampler object for No-U-Turn sampling, with the algorithm’s step size parameter adaptively tuned during burn-in iterations. Parameters are assumed to be continuous, but may be constrained or unconstrained.

Arguments

params : stochastic nodes to be updated with the sampler. Constrained parameters are mapped to unconstrained space according to transformations defined by the Stochastic link() function.

dtype : type of differentiation for gradient calculations. Options are

:central : central differencing.

:forward : forward differencing.

target : a target acceptance rate for the algorithm.

Value

Returns a Sampler type object.

Example

See the Examples section.