Slice Simplex (SliceSimplex)

Implementation of the slice simplex sampler as described by Cowles et al. [17] for simulating autocorrelated draws of parameters on the simplex 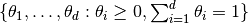and from a distribution that can be specified up to a constant of proportionality.

Model-Based Constructor

SliceSimplex(params::ElementOrVector{Symbol}; scale::Real=1.0)

Construct a Sampler object for which slice simplex sampling is to be applied separately to each of the supplied parameters. Parameters are assumed to be continuous and constrained to a simplex.

Arguments

• params : stochastic node(s) to be updated with the sampler.
• scale : value 0 < scale <= 1 by which to scale the standard simplex to define an initial space from which to simulate values.

Value

Returns a Sampler{SliceSimplexTune} type object.

Example

See the Asthma, Eyes, and other Examples.

Stand-Alone Function

slicesimplex!(v::SliceSimplexVariate, logf::Function; scale::Real=1.0)

Simulate one draw from a target distribution using a slice simplex sampler. Parameters are assumed to be continuous and constrained to a simplex.

Arguments

• v : current state of parameters to be simulated.
• scale : value 0 < scale <= 1 by which to scale the standard simplex to define an initial space from which to simulate values.
• logf : function that takes a single DenseVector argument of parameter values at which to compute the log-transformed density (up to a normalizing constant).

Value

Returns v updated with simulated values and associated tuning parameters.

Example

################################################################################
## Multinomial Model
##   y ~ Multinomial(n, rho)
##   rho ~ Dirichlet(1, ..., 1)
################################################################################

using Mamba

## Data
n, k = 100, 5
rho0 = rand(Dirichlet(ones(k)))
y = rand(Multinomial(n, rho0))

## Log-transformed Posterior(rho) + Constant
logf = function(rho::DenseVector)
  logpdf(Multinomial(n, rho), y)
end

## MCMC Simulation with Slice Simplex Sampling
t = 10000
sim = Chains(t, k, names = map(i -> "rho[$i]", 1:k))
rho = SliceSimplexVariate(fill(1 / k, k))
for i in 1:t
  slicesimplex!(rho, logf)
  sim[i, :, 1] = rho
end
describe(sim)

p = plot(sim)
draw(p, filename = "slicesimplexplot")

SliceSimplexVariate Type

Declaration

typealias SliceSimplexVariate SamplerVariate{SliceSimplexTune}

Fields

• value::Vector{Float64} : simulated values.
• tune::SliceSimplexTune : tuning parameters for the sampling algorithm.

Constructors

SliceSimplexVariate(x::AbstractVector{T<:Real})

SliceSimplexVariate(x::AbstractVector{T<:Real}, tune::SliceSimplexTune)

Construct a SliceSimplexVariate object that stores simulated values and tuning parameters for slice simplex sampling.

Arguments

• x : simulated values.
• tune : tuning parameters for the sampling algorithm. If not supplied, parameters are set to their defaults.

Value

Returns a SliceSimplexVariate type object with fields set to the values supplied to arguments x and tune.

SliceSimplexTune Type

Declaration

type SliceSimplexTune <: SamplerTune

Fields

• scale::Float64 : value 0 < scale <= 1 by which to scale the standard simplex to define an initial space from which to simulate values.