GK: Approximate Bayesian Computation

Approximate Bayesian Computation (ABC) is often useful when the likelihood is costly to compute. The generalized GK distribution [76] is a distribution defined by the inverse of its cumulative distribution function. It is therefore easy to sample from, but difficult to obtain analytical likelihood functions. These properties make the GK distribution well suited for ABC. The following is a simulation study that mirrors [1].

Model

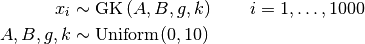
Analysis Program

using Distributed
@everywhere using Mamba

@everywhere extensions = quote
  using Distributions
  import Distributions: location, scale, skewness, kurtosis, minimum, maximum,
         quantile

  struct GK <: ContinuousUnivariateDistribution
    A::Float64
    B::Float64
    g::Float64
    k::Float64
    c::Float64

    function GK(A::Real, B::Real, g::Real, k::Real, c::Real)
      ## check args
      0.0 <= c < 1.0 || throw(ArgumentError("c must be in [0, 1)"))

      ## create distribution
      new(A, B, g, k, c)
    end

    GK(A::Real, B::Real, g::Real, k::Real) = GK(A, B, g, k, 0.8)
  end

  ## Parameters
  location(d::GK) = d.A
  scale(d::GK) = d.B
  skewness(d::GK) = d.g
  kurtosis(d::GK) = d.k
  asymmetry(d::GK) = d.c

  minimum(d::GK) = -Inf
  maximum(d::GK) = Inf

  function quantile(d::GK, p::Float64)
    z = quantile(Normal(), p)
    z2gk(d, z)
  end

  function z2gk(d::GK, z::Float64)
    term1 = exp(-skewness(d) * z)
    term2 = (1.0 + asymmetry(d) * (1.0 - term1) / (1.0 + term1))
    term3 = (1.0 + z^2)^kurtosis(d)
    location(d) + scale(d) * z * term2 * term3
  end
end

@everywhere eval(extensions)

d = GK(3, 1, 2, 0.5)
x = rand(d, 1000)

allingham = Dict{Symbol, Any}(
  :x => x
)

model = Model(
  x = Stochastic(1, (A, B, g, k) -> GK(A, B, g, k), false),
  A = Stochastic(() -> Uniform(0, 10)),
  B = Stochastic(() -> Uniform(0, 10)),
  g = Stochastic(() -> Uniform(0, 10)),
  k = Stochastic(() -> Uniform(0, 10))
)

inits = [
  Dict{Symbol, Any}(:x => x, :A => 3.5, :B => 0.5,
                    :g => 2.0, :k => 0.5),
  Dict{Symbol, Any}(:x => x, :A => median(x),
                    :B => sqrt(var(x)),
                    :g => 1.0, :k => 1.0),
  Dict{Symbol, Any}(:x => x, :A => median(x),
                    :B => diff(quantile(x, [0.25, 0.75]))[1],
                    :g => mean((x .- mean(x)).^3) / (var(x)^(3 / 2)),
                    :k => rand())
]

sigma1 = 0.05
sigma2 = 0.5
stats = x -> quantile(x, [0.1, 0.25, 0.5, 0.75, 0.9])
epsilon = 0.1

scheme = [ABC([:A, :B, :k],
              sigma1, stats, epsilon, maxdraw=50, decay=0.75, randeps=true),
          ABC(:g, sigma2, stats, epsilon, maxdraw=50, decay=0.75)]
setsamplers!(model, scheme)

sim = mcmc(model, allingham, inits, 10000, burnin=2500, chains=3)
describe(sim)
p = plot(sim)
draw(p, filename="gk")

Results

Iterations = 2501:10000
Thinning interval = 1
Chains = 1,2,3
Samples per chain = 7500

Empirical Posterior Estimates:
     Mean        SD        Naive SE       MCSE         ESS
k 0.3510874 0.132239097 0.00088159398 0.0082306353  258.13865
A 3.0037486 0.068834777 0.00045889851 0.0018699334 1355.07569
B 1.0575823 0.129916443 0.00086610962 0.0074502510  304.07900
g 2.0259195 0.311756472 0.00207837648 0.0114243024  744.68323

Quantiles:
     2.5%       25.0%      50.0%      75.0%     97.5%
k 0.12902213 0.25821839 0.34355889 0.42948590 0.6759640
A 2.86683504 2.95778075 3.00296541 3.04971216 3.1358843
B 0.80207071 0.96839859 1.05571418 1.14595782 1.3123378
g 1.56533594 1.79945626 1.97432281 2.19565833 2.7212103