Jaws: Repeated Measures Analysis of Variance¶
An example from OpenBUGS [44] and Elston and Grizzle [24] concerning jaw bone heights measured repeatedly in a cohort of 20 boys at ages 8, 8.5, 9, and 9.5 years.
Model¶
Bone heights are modelled as
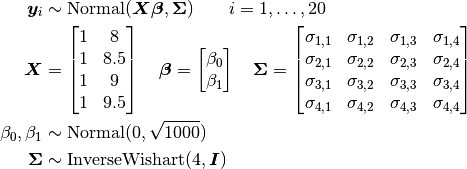
where 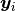 is a vector of the four repeated measurements for boy
is a vector of the four repeated measurements for boy 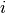 . In the model specification below, bone heights are arranged into a 1-dimensional vector on which a Block-Diagonal Multivariate Normal Distribution is specified. Also not that since
. In the model specification below, bone heights are arranged into a 1-dimensional vector on which a Block-Diagonal Multivariate Normal Distribution is specified. Also not that since 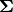 is a covariance matrix, it is symmetric with
is a covariance matrix, it is symmetric with M * (M + 1) / 2 unique (upper or lower triangular) parameters, where M is the matrix dimension.
Analysis Program¶
using Distributed
@everywhere using Mamba, LinearAlgebra
## Data
jaws = Dict{Symbol, Any}(
:Y =>
[47.8 48.8 49.0 49.7
46.4 47.3 47.7 48.4
46.3 46.8 47.8 48.5
45.1 45.3 46.1 47.2
47.6 48.5 48.9 49.3
52.5 53.2 53.3 53.7
51.2 53.0 54.3 54.5
49.8 50.0 50.3 52.7
48.1 50.8 52.3 54.4
45.0 47.0 47.3 48.3
51.2 51.4 51.6 51.9
48.5 49.2 53.0 55.5
52.1 52.8 53.7 55.0
48.2 48.9 49.3 49.8
49.6 50.4 51.2 51.8
50.7 51.7 52.7 53.3
47.2 47.7 48.4 49.5
53.3 54.6 55.1 55.3
46.2 47.5 48.1 48.4
46.3 47.6 51.3 51.8],
:age => [8.0, 8.5, 9.0, 9.5]
)
M = jaws[:M] = size(jaws[:Y], 2)
N = jaws[:N] = size(jaws[:Y], 1)
jaws[:y] = vec(jaws[:Y])
jaws[:x] = kron(ones(jaws[:N]), jaws[:age])
## Model Specification
model = Model(
y = Stochastic(1,
(beta0, beta1, x, Sigma) -> BDiagNormal(beta0 .+ beta1 * x, Sigma),
false
),
beta0 = Stochastic(
() -> Normal(0, sqrt(1000))
),
beta1 = Stochastic(
() -> Normal(0, sqrt(1000))
),
Sigma = Stochastic(2,
M -> InverseWishart(4.0, Matrix{Float64}(I, M, M))
)
)
## Initial Values
inits = [
Dict(:y => jaws[:y], :beta0 => 40, :beta1 => 1, :Sigma => Matrix{Float64}(I, M, M)),
Dict(:y => jaws[:y], :beta0 => 10, :beta1 => 10, :Sigma => Matrix{Float64}(I, M, M))
]
## Sampling Scheme
scheme = [Slice([:beta0, :beta1], [10, 1]),
AMWG(:Sigma, 0.1)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, jaws, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
Sigma[1,1] 6.7915801 2.0232463 0.0233624358 0.1421847433 202.48437
Sigma[1,2] 6.5982624 1.9670001 0.0227129612 0.1469366529 179.20433
Sigma[1,3] 6.1775526 1.9084389 0.0220367541 0.1532226770 155.13523
Sigma[1,4] 5.9477070 1.9358258 0.0223529913 0.1545185214 156.95367
Sigma[2,2] 6.9308723 2.0236387 0.0233669666 0.1531630007 174.56542
Sigma[2,3] 6.6005767 1.9885583 0.0229618936 0.1600864592 154.30055
Sigma[2,4] 6.3803028 2.0196017 0.0233203515 0.1612393116 156.88795
Sigma[3,3] 7.4564163 2.1925641 0.0253175499 0.1705734202 165.22733
Sigma[3,4] 7.4518620 2.2712194 0.0262257824 0.1733769737 171.60713
Sigma[4,4] 8.0594440 2.4746352 0.0285746264 0.1784057891 192.39975
beta1 1.8742617 0.2272166 0.0026236712 0.0071954415 997.16079
beta0 33.6379701 1.9912509 0.0229929845 0.0632742554 990.37090
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
Sigma[1,1] 3.7202164 5.3419070 6.5046777 7.8684049 11.5279247
Sigma[1,2] 3.5674344 5.2009878 6.3564397 7.6419462 11.2720602
Sigma[1,3] 3.2043099 4.8527075 5.9476859 7.1929746 10.8427648
Sigma[1,4] 2.9143241 4.5808041 5.6958961 6.9962164 10.6253935
Sigma[2,2] 3.7936234 5.4940524 6.6730872 8.0151463 11.6796110
Sigma[2,3] 3.4721419 5.2183567 6.3620683 7.6617912 11.4419940
Sigma[2,4] 3.2133129 4.9659531 6.1310937 7.4443619 11.3714037
Sigma[3,3] 4.1213458 5.9139585 7.1780478 8.6551856 12.8617596
Sigma[3,4] 4.0756709 5.8561719 7.1240011 8.7006336 13.0597624
Sigma[4,4] 4.4482953 6.3090779 7.6484712 9.4043857 14.0451233
beta1 1.4349627 1.7279142 1.8707215 2.0159440 2.3445976
beta0 29.4960557 32.3922780 33.6327451 34.9577696 37.4067853