Kidney: Weibull Regression with Random Effects¶
An example from OpenBUGS [44] and McGilchrist and Aisbett [62] concerning time to first and second infection recurrence in 38 kidney patients on dialysis.
Model¶
Time to recurrences are modelled as

where 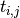 is the time of infection
is the time of infection 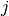 in patient
in patient 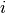 ,
, 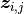 is a vector of covariates, and
is a vector of covariates, and 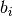 are patient-specific random effects.
are patient-specific random effects.
Analysis Program¶
using Distributed
@everywhere using Mamba
## Data
kidney = Dict{Symbol, Any}(
:t => permutedims(reshape(
[8, 16, 23, NaN, 22, 28, 447, 318, 30, 12, 24, 245, 7, 9, 511, 30, 53, 196,
15, 154, 7, 333, 141, NaN, 96, 38, NaN, NaN, 536, NaN, 17, NaN, 185, 177,
292, 114, NaN, NaN, 15, NaN, 152, 562, 402, NaN, 13, 66, 39, NaN, 12, 40,
NaN, 201, 132, 156, 34, 30, 2, 25, 130, 26, 27, 58, NaN, 43, 152, 30, 190,
NaN, 119, 8, NaN, NaN, NaN, 78, 63, NaN],
2, 38)),
:tcensor => permutedims(reshape(
[0, 0, 0, 13, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 8, 0,
0, 149, 70, 0, 25, 0, 4, 0, 0, 0, 0, 22, 159, 0, 108, 0, 0, 0, 24, 0, 0, 0,
46, 0, 0, 113, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 5, 0, 0, 54,
16, 6, 0, 0, 8],
2, 38)),
:age => permutedims(reshape(
[28, 28, 48, 48, 32, 32, 31, 32, 10, 10, 16, 17, 51, 51, 55, 56, 69, 69, 51,
52, 44, 44, 34, 34, 35, 35, 42, 42, 17, 17, 60, 60, 60, 60, 43, 44, 53, 53,
44, 44, 46, 47, 30, 30, 62, 63, 42, 43, 43, 43, 57, 58, 10, 10, 52, 52, 53,
53, 54, 54, 56, 56, 50, 51, 57, 57, 44, 45, 22, 22, 42, 42, 52, 52, 60, 60],
2, 38)),
:sex => [0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1,
1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
:disease => [1, 2, 1, 1, 1, 1, 2, 2, 3, 2, 3, 1, 3, 3, 1, 3, 1, 1, 2, 1, 4,
1, 3, 3, 3, 3, 2, 3, 2, 2, 3, 3, 4, 2, 1, 1, 4, 4],
:N => 38,
:M => 2
)
kidney[:Dx] = Int[
kidney[:disease][i] == j ? 1 : 0
for i in 1:38, j in 2:4
]
## Model Specification
model = Model(
t = Stochastic(2,
(alpha, beta_age, age, beta_sex, sex, Dx, beta_Dx, b, r, tcensor, N, M) ->
begin
beta_dis = Dx * beta_Dx
UnivariateDistribution[(
mu = alpha + beta_age * age[i, j] + beta_sex * sex[i] + beta_dis[i] +
b[i];
lambda = exp(-mu / r);
0 < lambda < Inf ?
Truncated(Weibull(r, lambda), tcensor[i, j], Inf) :
Uniform(0, Inf)) for i in 1:N, j in 1:M
]
end,
false
),
b = Stochastic(1,
s2 -> Normal(0, sqrt(s2)),
false
),
s2 = Stochastic(
() -> InverseGamma(0.001, 0.001)
),
alpha = Stochastic(
() -> Normal(0, 100)
),
beta_age = Stochastic(
() -> Normal(0, 100)
),
beta_sex = Stochastic(
() -> Normal(0, 100)
),
beta_Dx = Stochastic(1,
() -> Normal(0, 100)
),
r = Stochastic(
() -> Gamma(1, 1000)
)
)
## Initial Values
inits = [
Dict(:t => kidney[:t], :alpha => 0, :beta_age => 0, :beta_sex => 0,
:beta_Dx => zeros(3), :s2 => 3, :r => 1.0, :b => zeros(kidney[:N])),
Dict(:t => kidney[:t], :alpha => 1, :beta_age => -1, :beta_sex => 1,
:beta_Dx => ones(3), :s2 => 1, :r => 1.5, :b => zeros(kidney[:N]))
]
## Sampling Scheme
scheme = [MISS(:t),
Slice([:alpha, :beta_age, :beta_sex, :beta_Dx], 0.1),
Slice(:b, 0.01),
Slice(:s2, 0.1),
Slice(:r, 0.001)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, kidney, inits, 20000, burnin=2500, thin=2, chains=2)
describe(sim)