Dyes: Variance Components Model¶
An example from OpenBUGS [44], Davies [21], and Box and Tiao [8] concerning batch-to-batch variation in yields from six batches and five samples of dyestuff.
Analysis Program¶
using Distributed
@everywhere using Mamba, LinearAlgebra
## Data
dyes = Dict{Symbol, Any}(
:y =>
[1545, 1440, 1440, 1520, 1580,
1540, 1555, 1490, 1560, 1495,
1595, 1550, 1605, 1510, 1560,
1445, 1440, 1595, 1465, 1545,
1595, 1630, 1515, 1635, 1625,
1520, 1455, 1450, 1480, 1445],
:batches => 6,
:samples => 5
)
dyes[:batch] = vcat([fill(i, dyes[:samples]) for i in 1:dyes[:batches]]...)
dyes[:sample] = vcat(fill(collect(1:dyes[:samples]), dyes[:batches])...)
## Model Specification
model = Model(
y = Stochastic(1,
(mu, batch, s2_within) -> MvNormal(mu[batch], sqrt(s2_within)),
false
),
mu = Stochastic(1,
(theta, batches, s2_between) -> Normal(theta, sqrt(s2_between))
),
theta = Stochastic(
() -> Normal(0, 1000)
),
s2_within = Stochastic(
() -> InverseGamma(0.001, 0.001)
),
s2_between = Stochastic(
() -> InverseGamma(0.001, 0.001)
)
)
## Initial Values
inits = [
Dict(:y => dyes[:y], :theta => 1500, :s2_within => 1, :s2_between => 1,
:mu => fill(1500, dyes[:batches])),
Dict(:y => dyes[:y], :theta => 3000, :s2_within => 10, :s2_between => 10,
:mu => fill(3000, dyes[:batches]))
]
## Sampling Schemes
scheme = [NUTS([:mu, :theta]),
Slice([:s2_within, :s2_between], 1000.0)]
scheme2 = [MALA(:theta, 50.0),
MALA(:mu, 50.0, Matrix{Float64}(I, dyes[:batches], dyes[:batches])),
Slice([:s2_within, :s2_between], 1000.0)]
scheme3 = [HMC(:theta, 10.0, 5),
HMC(:mu, 10.0, 5, Matrix{Float64}(I, dyes[:batches], dyes[:batches])),
Slice([:s2_within, :s2_between], 1000.0)]
scheme4 = [RWM(:theta, 50.0, proposal=Cosine),
RWM(:mu, 50.0),
Slice([:s2_within, :s2_between], 1000.0)]
## MCMC Simulations
setsamplers!(model, scheme)
sim = mcmc(model, dyes, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
setsamplers!(model, scheme2)
sim2 = mcmc(model, dyes, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim2)
setsamplers!(model, scheme3)
sim3 = mcmc(model, dyes, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim3)
setsamplers!(model, scheme4)
sim4 = mcmc(model, dyes, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim4)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
s2_between 3192.2614 4456.129102 51.45494673 487.44961486 83.57109
theta 1526.7186 24.549671 0.28347518 0.37724897 3750.00000
s2_within 2887.5853 1075.174260 12.41504296 76.89117959 195.52607
mu[1] 1511.4798 20.819711 0.24040531 0.52158448 1593.30921
mu[2] 1527.9087 20.344151 0.23491402 0.30199960 3750.00000
mu[3] 1552.6742 21.293738 0.24587891 0.70276515 918.08605
mu[4] 1506.6440 21.349176 0.24651905 0.61821290 1192.57616
mu[5] 1578.6636 25.512471 0.29459264 1.29216105 389.82685
mu[6] 1487.1934 24.693967 0.28514137 1.23710390 398.44592
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
s2_between 111.92351 815.9012 1651.4605 3269.5663 1.90261752x104
theta 1475.08243 1513.5687 1527.1763 1540.0550 1.57444106x103
s2_within 1566.61796 2160.3251 2654.9358 3324.8621 5.65161862x103
mu[1] 1469.68693 1498.0985 1511.3084 1525.7344 1.55281296x103
mu[2] 1486.15990 1514.8487 1527.6843 1541.2155 1.56770562x103
mu[3] 1512.72912 1537.7046 1552.1976 1566.7188 1.59498301x103
mu[4] 1463.91701 1492.3206 1506.9856 1521.3449 1.54854165x103
mu[5] 1528.52480 1562.1831 1579.2515 1596.0167 1.62731017x103
mu[6] 1440.27721 1470.7983 1486.1844 1502.9911 1.54464614x103

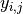 is the response for batch
is the response for batch 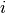 and sample
and sample 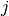 .
.