Stacks: Robust Regression¶
An example from OpenBUGS [44], Brownlee [14], and Birkes and Dodge [5] concerning 21 daily responses of stack loss, the amount of ammonia escaping, as a function of air flow, temperature, and acid concentration.
Analysis Program¶
using Distributed
@everywhere using Mamba
## Data
stacks = Dict{Symbol, Any}(
:y => [42, 37, 37, 28, 18, 18, 19, 20, 15, 14, 14, 13, 11, 12, 8, 7, 8, 8, 9,
15, 15],
:x =>
[80 27 89
80 27 88
75 25 90
62 24 87
62 22 87
62 23 87
62 24 93
62 24 93
58 23 87
58 18 80
58 18 89
58 17 88
58 18 82
58 19 93
50 18 89
50 18 86
50 19 72
50 19 79
50 20 80
56 20 82
70 20 91]
)
stacks[:N] = size(stacks[:x], 1)
stacks[:p] = size(stacks[:x], 2)
stacks[:meanx] = map(j -> mean(stacks[:x][:, j]), 1:stacks[:p])
stacks[:sdx] = map(j -> std(stacks[:x][:, j]), 1:stacks[:p])
stacks[:z] = Float64[
(stacks[:x][i, j] - stacks[:meanx][j]) / stacks[:sdx][j]
for i in 1:stacks[:N], j in 1:stacks[:p]
]
## Model Specification
model = Model(
y = Stochastic(1,
(mu, s2, N) ->
UnivariateDistribution[Laplace(mu[i], s2) for i in 1:N],
false
),
beta0 = Stochastic(
() -> Normal(0, 1000),
false
),
beta = Stochastic(1,
() -> Normal(0, 1000),
false
),
mu = Logical(1,
(beta0, z, beta) -> beta0 .+ z * beta,
false
),
s2 = Stochastic(
() -> InverseGamma(0.001, 0.001),
false
),
sigma = Logical(
s2 -> sqrt(2.0) * s2
),
b0 = Logical(
(beta0, b, meanx) -> beta0 - dot(b, meanx)
),
b = Logical(1,
(beta, sdx) -> beta ./ sdx
),
outlier = Logical(1,
(y, mu, sigma, N) ->
Float64[abs((y[i] - mu[i]) / sigma) > 2.5 for i in 1:N],
[1, 3, 4, 21]
)
)
## Initial Values
inits = [
Dict(:y => stacks[:y], :beta0 => 10, :beta => [0, 0, 0], :s2 => 10),
Dict(:y => stacks[:y], :beta0 => 1, :beta => [1, 1, 1], :s2 => 1)
]
## Sampling Scheme
scheme = [NUTS([:beta0, :beta]),
Slice(:s2, 1.0)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, stacks, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
b[1] 0.836863707 0.13085145 0.0015109423 0.0027601754 2247.4171
b[2] 0.744454449 0.33480007 0.0038659382 0.0065756939 2592.3158
b[3] -0.116648437 0.12214077 0.0014103601 0.0015143922 3750.0000
b0 -38.776564595 8.81860433 0.1018284717 0.0979006137 3750.0000
sigma 3.487643717 0.87610847 0.0101164292 0.0279025494 985.8889
outlier[1] 0.042666667 0.20211796 0.0023338572 0.0029490162 3750.0000
outlier[3] 0.054800000 0.22760463 0.0026281519 0.0034398827 3750.0000
outlier[4] 0.298000000 0.45740999 0.0052817156 0.0089200654 2629.5123
outlier[21] 0.606400000 0.48858046 0.0056416412 0.0113877443 1840.7583
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
b[1] 0.57218621 0.75741345 0.834874964 0.918345319 1.101502854
b[2] 0.16177144 0.52291878 0.714951465 0.933171533 1.476258382
b[3] -0.36401372 -0.19028697 -0.113463801 -0.036994963 0.118538277
b0 -56.70056875 -44.11785905 -38.698338454 -33.409149788 -21.453323631
sigma 2.17947513 2.86899865 3.348631697 3.953033535 5.592773118
outlier[1] 0.00000000 0.00000000 0.000000000 0.000000000 1.000000000
outlier[3] 0.00000000 0.00000000 0.000000000 0.000000000 1.000000000
outlier[4] 0.00000000 0.00000000 0.000000000 1.000000000 1.000000000
outlier[21] 0.00000000 0.00000000 1.000000000 1.000000000 1.000000000
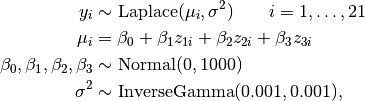
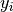 is the stack loss on day
is the stack loss on day 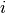 ; and
; and 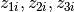 are standardized predictors.
are standardized predictors.