Leuk: Cox Regression¶
An example from OpenBUGS [44] and Ezzet and Whitehead [27] concerning survival in 42 leukemia patients treated with 6-mercaptopurine or placebo.
Model¶
Times to death are modelled using the Bayesian Cox proportional hazards model, formulated by Clayton [17] as
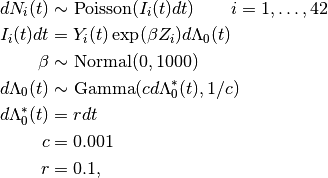
where 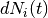 is a counting process increment in time interval
is a counting process increment in time interval 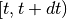 for patient
for patient 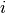 ;
; 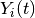 is an indicator of whether the patient is observed at time
is an indicator of whether the patient is observed at time 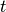 ;
; 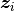 is a vector of covariates; and
is a vector of covariates; and 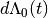 is the increment in the integrated baseline hazard function during
is the increment in the integrated baseline hazard function during 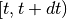 .
.
Analysis Program¶
using Distributed
@everywhere using Mamba
## Data
leuk = Dict{Symbol, Any}(
:t_obs =>
[1, 1, 2, 2, 3, 4, 4, 5, 5, 8, 8, 8, 8, 11, 11, 12, 12, 15, 17, 22, 23, 6,
6, 6, 6, 7, 9, 10, 10, 11, 13, 16, 17, 19, 20, 22, 23, 25, 32, 32, 34, 35],
:fail =>
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0,
1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
:Z =>
[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
0.5, 0.5, 0.5, 0.5, 0.5, 0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5,
-0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5, -0.5,
-0.5, -0.5],
:t => [1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 22, 23, 35]
)
leuk[:N] = N = length(leuk[:t_obs])
leuk[:T] = T = length(leuk[:t]) - 1
leuk[:Y] = Array{Int}(undef, N, T)
leuk[:dN] = Array{Int}(undef, N, T)
for i in 1:N
for j in 1:T
leuk[:dN][i, j] = leuk[:fail][i] * (leuk[:t_obs][i] == leuk[:t][j])
leuk[:Y][i, j] = Int(leuk[:t_obs][i] >= leuk[:t][j])
end
end
leuk[:c] = 0.001
leuk[:r] = 0.1
## Model Specification
model = Model(
dN = Stochastic(2,
(Y, beta, Z, dL0, N, T) ->
UnivariateDistribution[
Y[i, j] > 0 ? Poisson(exp(beta * Z[i]) * dL0[j]) : Flat()
for i in 1:N, j in 1:T
],
false
),
mu = Logical(1,
(c, r, t) -> c * r * (t[2:end] - t[1:(end - 1)]),
false
),
dL0 = Stochastic(1,
(mu, c, T) -> UnivariateDistribution[Gamma(mu[j], 1 / c) for j in 1:T],
false
),
beta = Stochastic(
() -> Normal(0, 1000)
),
S0 = Logical(1,
dL0 -> exp.(-cumsum(dL0)),
false
),
S_treat = Logical(1,
(S0, beta) -> S0.^exp(-0.5 * beta)
),
S_placebo = Logical(1,
(S0, beta) -> S0.^exp(0.5 * beta)
)
)
## Initial Values
inits = [
Dict(:dN => leuk[:dN], :beta => 0, :dL0 => fill(1, leuk[:T])),
Dict(:dN => leuk[:dN], :beta => 1, :dL0 => fill(2, leuk[:T]))
]
## Sampling Scheme
scheme = [AMWG(:dL0, 0.1),
Slice(:beta, 3.0)]
setsamplers!(model, scheme)
## MCMC Simulations
sim = mcmc(model, leuk, inits, 10000, burnin=2500, thin=2, chains=2)
describe(sim)
Results¶
Iterations = 2502:10000
Thinning interval = 2
Chains = 1,2
Samples per chain = 3750
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
beta 1.552064427 0.424977799 0.00490722093 0.0121343026 1226.59967
S_treat[1] 0.983021837 0.014032858 0.00016203749 0.0006444873 474.09293
S_treat[2] 0.966246426 0.020819923 0.00024040776 0.0009762155 454.84854
S_treat[3] 0.956207131 0.024534430 0.00028329919 0.0011874261 426.91239
S_treat[4] 0.936432950 0.031636973 0.00036531230 0.0015140463 436.62796
S_treat[5] 0.913982241 0.037982886 0.00043858859 0.0017354084 479.04081
S_treat[6] 0.879372323 0.047653044 0.00055024996 0.0021437962 494.09936
S_treat[7] 0.867528817 0.051602796 0.00059585777 0.0024545959 441.96358
S_treat[8] 0.821750962 0.064689997 0.00074697574 0.0030256573 457.12479
S_treat[9] 0.805557685 0.068612901 0.00079227353 0.0032183437 454.51343
S_treat[10] 0.771831536 0.076942474 0.00088845517 0.0035776788 462.51903
S_treat[11] 0.735657019 0.085534730 0.00098766999 0.0040566359 444.58306
S_treat[12] 0.712600209 0.089598298 0.00103459203 0.0040292944 494.47179
S_treat[13] 0.691135357 0.094685927 0.00109333891 0.0044879053 445.12656
S_treat[14] 0.664423491 0.098857036 0.00114150273 0.0046673584 448.61405
S_treat[15] 0.636423003 0.102857125 0.00118769178 0.0047872478 461.63310
S_treat[16] 0.565616003 0.112893079 0.00130357699 0.0049341458 523.49276
S_treat[17] 0.471034334 0.120102602 0.00138682539 0.0050776645 559.47003
S_placebo[1] 0.927789861 0.050170096 0.00057931437 0.0023120443 470.86627
S_placebo[2] 0.859431833 0.067291385 0.00077701399 0.0030529117 485.83685
S_placebo[3] 0.820804570 0.074342778 0.00085843646 0.0034349005 468.43490
S_placebo[4] 0.748344200 0.085488930 0.00098714114 0.0038433955 494.75434
S_placebo[5] 0.671088723 0.090818803 0.00104868521 0.0036921538 605.05098
S_placebo[6] 0.564655613 0.097783399 0.00112910544 0.0038182815 655.83466
S_placebo[7] 0.532173306 0.099628193 0.00115040728 0.0042364979 553.03234
S_placebo[8] 0.418874416 0.097451300 0.00112527068 0.0038432054 642.96611
S_placebo[9] 0.383210551 0.095687796 0.00110490749 0.0036248738 696.83078
S_placebo[10] 0.317122087 0.091201496 0.00105310416 0.0031779306 823.59766
S_placebo[11] 0.256739191 0.086400289 0.00099766461 0.0029358329 866.09938
S_placebo[12] 0.223014153 0.082260904 0.00094986710 0.0026813211 941.21603
S_placebo[13] 0.195547225 0.079430544 0.00091718492 0.0029106845 744.70591
S_placebo[14] 0.164855445 0.074276591 0.00085767220 0.0026970503 758.44802
S_placebo[15] 0.137032754 0.068763778 0.00079401571 0.0026184621 689.64703
S_placebo[16] 0.083796000 0.054748991 0.00063218689 0.0020660044 702.24679
S_placebo[17] 0.040920336 0.037737842 0.00043575906 0.0012818385 866.73735
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
beta 0.7524244645 1.259092877 1.540715015 1.829373993 2.41862572
S_treat[1] 0.9462141591 0.977211258 0.986955387 0.992864719 0.99836877
S_treat[2] 0.9150951603 0.955732194 0.970764331 0.981528195 0.99312428
S_treat[3] 0.8974993157 0.943194903 0.960671242 0.974341293 0.98958205
S_treat[4] 0.8599068641 0.919023530 0.941699242 0.959578177 0.98196246
S_treat[5] 0.8239755135 0.892499135 0.919841738 0.941506275 0.97166964
S_treat[6] 0.7738755125 0.850772834 0.885177533 0.913944652 0.95521105
S_treat[7] 0.7531822416 0.836159276 0.873267366 0.904856224 0.95037821
S_treat[8] 0.6801713643 0.780967298 0.828861810 0.868789540 0.92883388
S_treat[9] 0.6555328459 0.762836917 0.813277192 0.854664506 0.91930265
S_treat[10] 0.6026848684 0.723608005 0.779448002 0.826762737 0.90169913
S_treat[11] 0.5503082957 0.681881638 0.743447395 0.797449392 0.87990722
S_treat[12] 0.5233565529 0.654970518 0.720927823 0.777608202 0.86466162
S_treat[13] 0.4922868942 0.631085044 0.699537585 0.758920006 0.85262814
S_treat[14] 0.4597297883 0.598392933 0.670665550 0.735415731 0.83825032
S_treat[15] 0.4269750729 0.566537132 0.641228870 0.709931594 0.82208295
S_treat[16] 0.3438735907 0.487880437 0.566936069 0.644918756 0.77749139
S_treat[17] 0.2466734959 0.383395600 0.469857377 0.555064846 0.70280881
S_placebo[1] 0.7997904171 0.903185030 0.939595572 0.964924422 0.99089079
S_placebo[2] 0.7055958749 0.819313313 0.869352795 0.908385797 0.96318697
S_placebo[3] 0.6563988800 0.773124226 0.828159645 0.876023887 0.94337131
S_placebo[4] 0.5660793194 0.692444549 0.754818343 0.810412223 0.89462480
S_placebo[5] 0.4851605247 0.609481976 0.675431460 0.736195314 0.83615527
S_placebo[6] 0.3696872931 0.497149446 0.566089714 0.632288659 0.74932879
S_placebo[7] 0.3402856402 0.462939149 0.532290556 0.601897323 0.72484128
S_placebo[8] 0.2379614336 0.349405859 0.415075601 0.483568964 0.62050327
S_placebo[9] 0.2091293870 0.314947858 0.378301304 0.447909630 0.58210955
S_placebo[10] 0.1562465305 0.250265102 0.311673305 0.378896633 0.51089391
S_placebo[11] 0.1092657207 0.193262012 0.249637651 0.312589668 0.44360059
S_placebo[12] 0.0845659713 0.162032458 0.216266931 0.276356661 0.40448425
S_placebo[13] 0.0650227582 0.137218626 0.187654643 0.246139543 0.37311156
S_placebo[14] 0.0479431220 0.110429658 0.156032281 0.209723502 0.33168432
S_placebo[15] 0.0342784539 0.086171750 0.127242826 0.176712122 0.29500763
S_placebo[16] 0.0125569906 0.042952635 0.072131767 0.112032446 0.22046612
S_placebo[17] 0.0021678381 0.013959709 0.029822826 0.055822282 0.14078639